题目内容
 如图,直线AB⊥平面BCD,∠BCD=90°,则图中直角三角形的个数为
如图,直线AB⊥平面BCD,∠BCD=90°,则图中直角三角形的个数为4
4
.分析:将条件直线AB⊥平面BCD进行转化,线面垂直⇒线线垂直.易得△ABC是直角三角形,△ABD是直角三角形,再结合∠BCD=90°⇒DC⊥面ABC⇒△ACD是直角三角形.
解答:解:由题意AB⊥平面BCD,由直线和平面垂直的定义
∴①AB⊥BC,⇒△ABC是直角三角形
②AB⊥BD,⇒△ABD是直角三角形
又 ③∠BCD=90°△BCD是直角三角形
④AB⊥平面BCD⇒AB⊥DC,又BC⊥DC,
由直线和平面垂直的判定定理,得 DC⊥面ABC,
∴DC⊥AC⇒△ACD是直角三角形
故答案为4.
∴①AB⊥BC,⇒△ABC是直角三角形
②AB⊥BD,⇒△ABD是直角三角形
又 ③∠BCD=90°△BCD是直角三角形
④AB⊥平面BCD⇒AB⊥DC,又BC⊥DC,
由直线和平面垂直的判定定理,得 DC⊥面ABC,
∴DC⊥AC⇒△ACD是直角三角形
故答案为4.
点评:本题考查棱锥的结构特征,求解本题的关键是对棱锥中的点线面的位置关系有着比较熟悉的了解,且能根据其已知的位置关系作出一些判断得出新的结论,本题考查了空间想像能力以及推理论证的能力.空间问题问题平面问题相互转化的能力.

练习册系列答案
相关题目
 如图,直线l⊥平面α,垂足为O,已知长方体ABCD-A1B1C1D1中,AA1=5,AB=6,AD=8.该长方体做符合以下条件的自由运动:(1)A∈l;(2)C∈α,则C1、O两点间的最大距离为
如图,直线l⊥平面α,垂足为O,已知长方体ABCD-A1B1C1D1中,AA1=5,AB=6,AD=8.该长方体做符合以下条件的自由运动:(1)A∈l;(2)C∈α,则C1、O两点间的最大距离为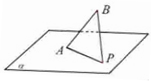 如图,直线AB是平面α的斜线,A为斜足,若点P在平面α内运动,使得点P到直线AB的距离为定值a(a>0),则动点P的轨迹是( )
如图,直线AB是平面α的斜线,A为斜足,若点P在平面α内运动,使得点P到直线AB的距离为定值a(a>0),则动点P的轨迹是( ) 如图,直线AB⊥平面BCD,∠BCD=90°,则图中直角三角形的个数为________.
如图,直线AB⊥平面BCD,∠BCD=90°,则图中直角三角形的个数为________.