题目内容
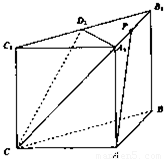
已知ABC-A1B1C1是各条棱长均等于a的正三棱柱,D是侧棱CC1的中点.点C1到平面AB1D的距离( )
A.

B.

C.

D.

【答案】分析:以A为原点,以垂直AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,则 ,
, ,
, ,设平面AB1D的法向量
,设平面AB1D的法向量 ,由
,由 ,知
,知 =(
=( ),由向量法能求出C1到平面AB1D的距离.
),由向量法能求出C1到平面AB1D的距离.
解答: 解:以A为原点,以垂直AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,
解:以A为原点,以垂直AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,
∵ABC-A1B1C1是各条棱长均等于a的正三棱柱,D是侧棱CC1的中点,
∴A(0,0,0), ,D(0,a,
,D(0,a, ),C1(0,a,a),
),C1(0,a,a),
∴ ,
, ,
, ,
,
设平面AB1D的法向量 ,
,
∵ ,
,
∴ ,
,
∴ =(
=( )
)
∴C1到平面AB1D的距离 =
= =
= .
.
故选A.
点评:本题考查点到平面的距离的求法,是基础题.解题时要认真审题,仔细解答,注意向量法的合理运用.
 ,
, ,
, ,设平面AB1D的法向量
,设平面AB1D的法向量 ,由
,由 ,知
,知 =(
=( ),由向量法能求出C1到平面AB1D的距离.
),由向量法能求出C1到平面AB1D的距离.解答:
 解:以A为原点,以垂直AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,
解:以A为原点,以垂直AC的直线为x轴,以AC为y轴,以AA1为z轴,建立空间直角坐标系,∵ABC-A1B1C1是各条棱长均等于a的正三棱柱,D是侧棱CC1的中点,
∴A(0,0,0),
 ,D(0,a,
,D(0,a, ),C1(0,a,a),
),C1(0,a,a),∴
 ,
, ,
, ,
,设平面AB1D的法向量
 ,
,∵
 ,
,∴
 ,
,∴
 =(
=( )
)∴C1到平面AB1D的距离
 =
= =
= .
.故选A.
点评:本题考查点到平面的距离的求法,是基础题.解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
相关题目
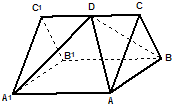 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点. 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.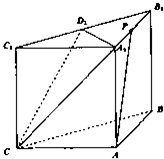 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.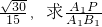 的值.
的值.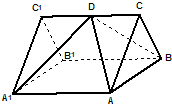
 的值.
的值.