题目内容
若三点P(1,1),A(2,-4),B(x,-9)共线,则( )
| A、x=-1 | ||
| B、x=3 | ||
C、x=
| ||
| D、x=1 |
分析:三点共线等价于以三点为起点终点的两个向量共线,利用向量坐标公式求出两个向量的坐标,利用向量共线的充要条件列出方程求出x.
解答:解:三点P(1,1),A(2,-4),B(x,-9)共线 ⇒
∥
,
=(1,-5),
=(x-1,-10),
⇒1×(-10)=-5(x-1)⇒x=3
故选B.
| PA |
| PB |
| PA |
| PB |
⇒1×(-10)=-5(x-1)⇒x=3
故选B.
点评:本题考查向量坐标的求法、考查向量共线的坐标形式的充要条件:坐标交叉相乘相等.也可以利用斜率相等解答,三角形的面积为0;点到直线的距离为0等等解答本题,方法多.

练习册系列答案
相关题目
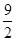 D、x=51
D、x=51