题目内容
16．已知函数f（x）是定义在区间[2，+∞）上的减函数，若f（a2-2）-f（2-3a）＞0成立，求实数a的范围．分析 根据函数单调性的性质建立不等式关系进行求解即可得到结论．
解答 解：若f（a2-2）-f（2-3a）＞0得若f（a2-2）＞f（2-3a），
∵函数f（x）是定义在区间[2，+∞）上的减函数，
∴$\left\{\begin{array}{l}{{a}^{2}-2≥2}\\{2-3a≥2}\\{{a}^{2}-2＜2-3a}\end{array}\right.$，即$\left\{\begin{array}{l}{{a}^{2}≥4}\\{a≤0}\\{{a}^{2}+3a-4＜0}\end{array}\right.$，
即$\left\{\begin{array}{l}{a≥2或a≤-2}\\{a≤0}\\{-4＜a＜1}\end{array}\right.$，得-4＜a≤-2，
即实数a的取值范围是（-4，-2]．
点评 本题主要考查不等式的求解，根据函数单调性的性质是解决本题的关键．注意定义域的限制作用．
练习册系列答案
阅读快车系列答案
相关题目
8．
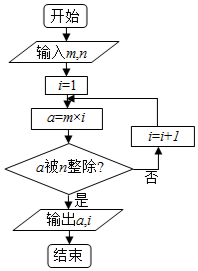当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）
当m=4，n=3时，运行如图所示的程序框图，将输出的a、i代入二项式（x2-$\frac{i}{x}$）a中，则此二项式的展开式中含x3项的系数为（ ）| A． | 37${C}_{12}^{7}$ | B． | 38${C}_{12}^{8}$ | C． | -33${C}_{12}^{3}$ | D． | -37${C}_{12}^{5}$ |