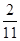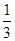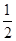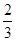题目内容
某商场为了了解毛衣的月销售量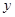 (件)与月平均气温
(件)与月平均气温 之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 | 17 | 13 | 8 | 2 |
月销售量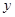 (件) (件) | 24 | 33 | 40 | 55 |
 中的
中的 =
= ,气象部门预测下个月的平均气温约为
,气象部门预测下个月的平均气温约为 ,据此估计该商场下个月毛衣销售量约为( )件.
,据此估计该商场下个月毛衣销售量约为( )件.A.58 B.40 C.38 D.46
D
解析试题分析:方法一:欲求在下个月的平均气温约为 时衣服的销售件数,考虑到线性回归方程
时衣服的销售件数,考虑到线性回归方程 中的
中的 =
= ,若能求出
,若能求出 ,将代入
,将代入 便可可出
便可可出 ,即服装件数.由数据表中可知,
,即服装件数.由数据表中可知, ,则
,则 ,即有
,即有 ,代入
,代入 ,得件数为46.此方法计算量较大,且易算错.方法二:考虑到统计学大多都含有估算的数学思想,所以可以尝试用估算法.由表可以知道,随着温度的降低,月销售量回增加.当温度为
,得件数为46.此方法计算量较大,且易算错.方法二:考虑到统计学大多都含有估算的数学思想,所以可以尝试用估算法.由表可以知道,随着温度的降低,月销售量回增加.当温度为 时,销售量应该介于40与55之间,而只有D符合条件,故选D.
时,销售量应该介于40与55之间,而只有D符合条件,故选D.
考点:回归直线方程的应用.

练习册系列答案
相关题目
统计某校1000名学生的数学水平测试成绩,得到样本频率分布直方图如图所示,若满分为100分,规定不低于60分为及格,则及格率是( )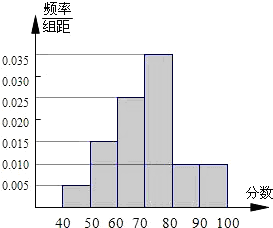
| A.20% | B.25% | C.6% | D.80% |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.28 | B.32 | C.64 | D.128 |
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
(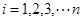 ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加 |
D.若该大学某女生身高为 ,则可断定其体重为 ,则可断定其体重为 |
某全日制大学共有学生5600人,其中专科生有1300人,本科生有3000人,研究生有1300人,现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为280人,则应在专科生、本科生与研究生这三类学生中分别抽取( )人.
| A.65,150,65 | B.30,150,100 | C.93,94,93 | D.80,120,80 |
已知样本7,10,14,8,7,12,11,10,8,10,13,10,8,11,8,9,12,9,13,20,那么这组数据落在8.5~11.5的频率为( )
| A.0.5 | B.0.4 | C.0.3 | D.0.2 |
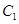 的参数方程为
的参数方程为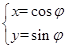 (
( 为参数),以坐标原点
为参数),以坐标原点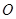 为极点,
为极点,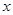 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆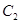 的极坐标方程为
的极坐标方程为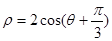 .
. ,则m的值为
,则m的值为 D、6.8
D、6.8