题目内容
直三棱ABC-A1B1C1的各顶点都在同一球面上，若，AB=AC=3，AA1=2，∠BAC=60°，则此球的表面积等于（ ）
| A、4π | B、8π | C、12π | D、16π |
分析：画出球的内接直三棱ABC-A1B1C1，作出球的半径，然后可求球的表面积．
解答：
解：直三棱ABC-A1B1C1的各顶点都在同一球面上，若，AB=AC=3，AA1=2，∠BAC=60°，
如图，连接上下底面中心，O为PQ的中点，OP⊥平面ABC，则球的半径为OA，
由题意OP=1，AP=
，OA=2，
所以球的表面积为：16π
故选D．
解：直三棱ABC-A1B1C1的各顶点都在同一球面上，若，AB=AC=3，AA1=2，∠BAC=60°，如图，连接上下底面中心，O为PQ的中点，OP⊥平面ABC，则球的半径为OA，
由题意OP=1，AP=
| 3 |
所以球的表面积为：16π
故选D．
点评：本题考查球的体积和表面积，球的内接体问题，考查学生空间想象能力理解失误能力，是基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
直三棱柱ABC-A1B1C1中，若
=a
=b
=c 则
=（ ）
| CA |
| CB |
| CC1 |
| A1B |
| A、a+b-c |
| B、a-b+c |
| C、-a+b+c |
| D、-a+b-c |
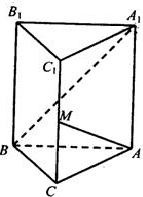如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，∠BAC=30°，BC=1，
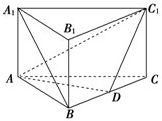（2012•黄州区模拟）如图，在直三棱柱ABC-A1B1C1中，AB=BC=2AA1，∠ABC=90°，D是BC的中点．
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．