题目内容
已知函数 的图象的一部分如下图所示.
的图象的一部分如下图所示.

(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)当 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
【答案】
(Ⅰ)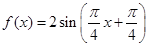 ;(Ⅱ)
;(Ⅱ) 时,
时,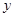 的最大值为
的最大值为 ;当
;当 ,即
,即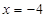 时,
时,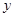 的最小值-2
的最小值-2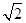 .
.
【解析】
试题分析:(Ⅰ)首先观察图像可得 ,
, ,利用公式
,利用公式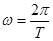 ,可求得
,可求得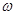 ,又图象经过点
,又图象经过点 ,利用代入法可求得
,利用代入法可求得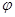 的值(也可以利用关键点法),从而可求得函数
的值(也可以利用关键点法),从而可求得函数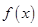 的解析式;(Ⅱ)由(Ⅰ)知,
的解析式;(Ⅱ)由(Ⅰ)知,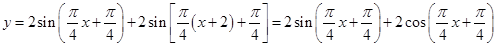 ,化简此函数的表达式,得
,化简此函数的表达式,得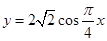 ,根据已知条件:∵
,根据已知条件:∵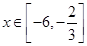 ,可得
,可得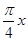 的取值范围,进而可求得
的取值范围,进而可求得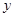 的最大值及最小值.
的最大值及最小值.
试题解析:(Ⅰ)由图像知 1分
1分
 3分
3分
得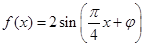 ,由对应点得,当
,由对应点得,当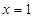 时,
时,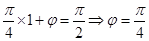 . 5分
. 5分
∴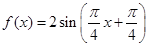 6分
6分
(Ⅱ)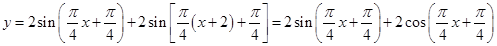
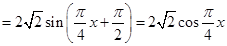 9分
9分
∵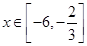 ,∴
,∴ ,∴当
,∴当 ,即
,即 时,
时,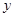 的最大值为
的最大值为 ;
;
当 ,即
,即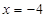 时,
时,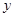 的最小值-2
的最小值-2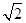 .
12分
.
12分
考点:1.三角函数的图像及其性质;2.三角函数的最值问题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
 x(A>0,
x(A>0,
 [0,4]的图象,且图象的最高点为S(3,2
[0,4]的图象,且图象的最高点为S(3,2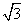 );赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定
);赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定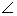 MNP=120
MNP=120
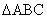 中
中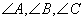 所对的边分别为
所对的边分别为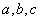 ;满足:
;满足: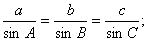
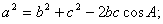
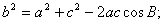
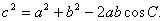 )
)