题目内容
（2011•泉州模拟）设奇函数f（x）在（0，+∞）上为增函数，且f（10）=0，则不等式
＜0的解集为（ ）
| f(x) |
| x |
分析：由题意可得x∈（0，10）时，f（x）＜0； x∈（10，+∞）时，f（x）＞0．再由函数f（x）是奇函数，
x∈（-10，0）时，f（x）＞0； x∈（-∞，-10）时，f（x）＜0．再由不等式可得
，或
．
由此求得原不等式的解集．
x∈（-10，0）时，f（x）＞0； x∈（-∞，-10）时，f（x）＜0．再由不等式可得
|
|
由此求得原不等式的解集．
解答：解：∵f（x）在（0，+∞）上为增函数，且f（10）=0，
∴x∈（0，10）时，f（x）＜0； x∈（10，+∞）时，f（x）＞0．
再由函数f（x）是奇函数，其图象关于原点对称可得，
x∈（-10，0）时，f（x）＞0； x∈（-∞，-10）时，f（x）＜0．
由不等式
＜0 可得
，或
．
由此解得 0＜x＜10，或-10＜x＜0．
故选D．
∴x∈（0，10）时，f（x）＜0； x∈（10，+∞）时，f（x）＞0．
再由函数f（x）是奇函数，其图象关于原点对称可得，
x∈（-10，0）时，f（x）＞0； x∈（-∞，-10）时，f（x）＜0．
由不等式
| f(x) |
| x |
|
|
由此解得 0＜x＜10，或-10＜x＜0．
故选D．
点评：本题主要考查函数的单调性和奇偶性的应用，分式不等式的解法，属于中档题．
练习册系列答案
相关题目
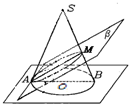（2011•泉州模拟）如图所示，圆锥SO的轴截面△SAB是边长为4的正三角形，M为母线SB的中点，过直线AM作平面β⊥面SAB，设β与圆锥侧面的交线为椭圆C，则椭圆C的短半轴为（ ）