题目内容
已知向量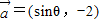 与
与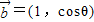 互相垂直,其中
互相垂直,其中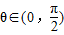
(1)求sinθ和cosθ的值
(2)若
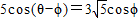 ,0<ϕ<
,0<ϕ<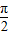 ,求cosϕ的值.
,求cosϕ的值.
【答案】分析:(1)由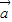
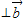 得到sinθ=2cosθ,再结合sin2θ+cos2θ=1求出sinθ和cosθ的值;
得到sinθ=2cosθ,再结合sin2θ+cos2θ=1求出sinθ和cosθ的值;
(2)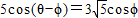 ,对等式左边用余弦的差角公式展开,得到cosφ=sinφ再有sin2φ+cos2φ=1,及0<φ<
,对等式左边用余弦的差角公式展开,得到cosφ=sinφ再有sin2φ+cos2φ=1,及0<φ<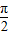 求得cosφ的值
求得cosφ的值
解答:解:(1)∵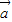
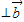 ,
,
∴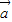 •
•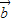 =sinθ-2cosθ=0,即sinθ=2cosθ…(2分)
=sinθ-2cosθ=0,即sinθ=2cosθ…(2分)
又∵sin2θ+cos2θ=1,
∴4cos2θ+cos2θ=1,即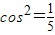 ,
,
∴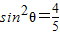 …(4分)
…(4分)
又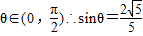 ,
,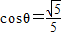 …(6分)
…(6分)
(2)∵5cos(θ-φ)=5(cosθcosφ+sinθsinφ)=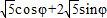 =
=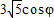 …(8分)
…(8分)
∴cosφ=sinφ,
∴cos2φ=sin2φ=1-cos2φ,
即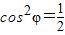 …(10分)
…(10分)
又 0<φ<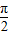 ,
,
∴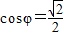 …(12分)
…(12分)
点评:本题考查数量积判断两个平面向量的垂直关系,解题的关键是理解向量垂直的坐标表示公式,以及能熟练利用同角三角函数的基本关系求三角函数值,解本题时要注意隐含条件sin2θ+cos2θ=1的运用,本题考查了变形与计算的能力
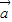
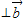 得到sinθ=2cosθ,再结合sin2θ+cos2θ=1求出sinθ和cosθ的值;
得到sinθ=2cosθ,再结合sin2θ+cos2θ=1求出sinθ和cosθ的值;(2)
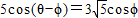 ,对等式左边用余弦的差角公式展开,得到cosφ=sinφ再有sin2φ+cos2φ=1,及0<φ<
,对等式左边用余弦的差角公式展开,得到cosφ=sinφ再有sin2φ+cos2φ=1,及0<φ<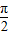 求得cosφ的值
求得cosφ的值解答:解:(1)∵
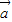
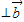 ,
,∴
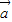 •
•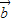 =sinθ-2cosθ=0,即sinθ=2cosθ…(2分)
=sinθ-2cosθ=0,即sinθ=2cosθ…(2分)又∵sin2θ+cos2θ=1,
∴4cos2θ+cos2θ=1,即
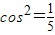 ,
,∴
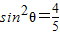 …(4分)
…(4分)又
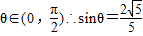 ,
,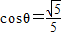 …(6分)
…(6分)(2)∵5cos(θ-φ)=5(cosθcosφ+sinθsinφ)=
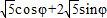 =
=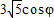 …(8分)
…(8分)∴cosφ=sinφ,
∴cos2φ=sin2φ=1-cos2φ,
即
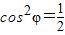 …(10分)
…(10分)又 0<φ<
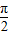 ,
,∴
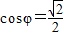 …(12分)
…(12分)点评:本题考查数量积判断两个平面向量的垂直关系,解题的关键是理解向量垂直的坐标表示公式,以及能熟练利用同角三角函数的基本关系求三角函数值,解本题时要注意隐含条件sin2θ+cos2θ=1的运用,本题考查了变形与计算的能力

练习册系列答案
相关题目
 与
与 互相垂直,其中
互相垂直,其中 .
. 和
和 的值;
的值; ,
, ,求
,求 的值.
的值. 与
与
 _________
_________ 与
与 互相垂直,其中
互相垂直,其中 .
. 和
和 的值;②若
的值;②若 ,求
,求 的值.
的值.