题目内容
已知 是
是 的一个极值点.
的一个极值点.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 求函数 的单调递减区间;
的单调递减区间;
(Ⅲ)设 ,试问过点
,试问过点 可作多少条直线与曲线
可作多少条直线与曲线 相切?请说明理由.
相切?请说明理由.
(Ⅰ)3;(Ⅱ)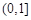 ;(Ⅲ)2条.
;(Ⅲ)2条.
解析试题分析:(Ⅰ)先对原函数求导,则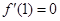 ,即得
,即得 的值;(Ⅱ)求当
的值;(Ⅱ)求当 时的
时的 的取值范围,就得函数的单调减区间;(Ⅲ)易知
的取值范围,就得函数的单调减区间;(Ⅲ)易知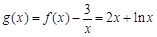 ,设过点(2,5)与曲线
,设过点(2,5)与曲线 相切的切点为
相切的切点为 ,
,
所以 ,
,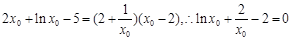 ,令
,令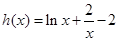 ,利用导数求函数
,利用导数求函数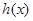 的单调区间及极值,可得
的单调区间及极值,可得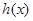 与
与 轴的交点个数,从而得结论.
轴的交点个数,从而得结论.
试题解析:(I)因为 是
是 的一个极值点,所
的一个极值点,所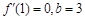 ,
,
经检验,适合题意,所以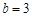 . 3分
. 3分
(II)定义域为 ,
,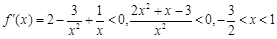 ,
,
所以函数的单调递减区间为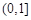 6分
6分
(III)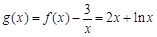 ,设过点(2,5)与曲线
,设过点(2,5)与曲线 相切的切点为
相切的切点为
所以 ,
,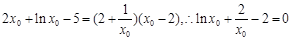 9分
9分
令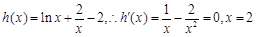 ,所
,所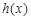 在
在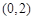 上单调递减,在
上单调递减,在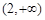 上单调递增,
上单调递增,
因为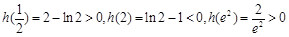 ,所以
,所以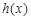 与x轴有两个交点,
与x轴有两个交点,
所以过点 可作2条直线与曲线
可作2条直线与曲线 相切. 12分
相切. 12分
考点:1、利用导数求函数的极值和单调性;2、导数与基本函数的综合应用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目

 的值域;
的值域; ,函数
,函数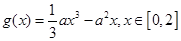 .若对任意
.若对任意 ,总存在
,总存在 ,使
,使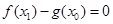 ,求实数
,求实数 的取值范围.
的取值范围.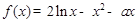 .
.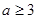 时,讨论函数
时,讨论函数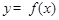 在[
在[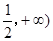 上的单调性;
上的单调性;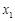 ,
,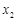
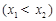 是函数
是函数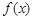 的两个零点,
的两个零点,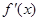 为函数
为函数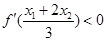 .
. .
.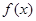 的单调区间;
的单调区间; 在
在 内恒成立,求实数
内恒成立,求实数 的取值范围.
的取值范围. ,求证:
,求证: .
. 是定义在
是定义在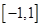 上的奇函数,在
上的奇函数,在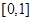 上
上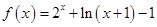 .
. .
. .
. 的单调性;
的单调性; 恒成立,证明:当
恒成立,证明:当 时,
时, .
.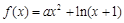 .
.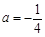 时,求函数
时,求函数 的单调区间;
的单调区间;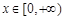 时,不等式
时,不等式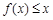 恒成立,求实数
恒成立,求实数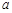 的取值范围.
的取值范围.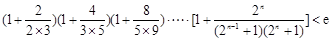 (
(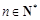 ,e是自然对数的底数).
,e是自然对数的底数). -
-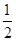 alnx,a∈R.
alnx,a∈R. )≤
)≤ ≤φ′(
≤φ′( ).
). (
( 为常数)
为常数)  的单调区间;
的单调区间; 时,
时, ,求
,求