题目内容
已知回归直线斜率的估计值为1.23，样本点的中心为点(4,5)，则回归直线的方程为( )
A.
＝1.23x＋4 B.＝1.23x＋5
C＝1.23x＋0.08 D.＝0.08x＋1.23
C
解析试题分析：本题考查线性回归直线方程，可根据回归直线方程一定经过样本中心点这一信息，选择验证法或排除法解决，具体方法就是将点（4，5）的坐标分别代入各个选项，满足的即为所求解：法一：由回归直线的斜率的估计值为1.23，可排除D由线性回归直线方程样本点的中心为（4，5），将x=4分别代入A、B、C，其值依次为8.92、9.92、5，排除A、B法二：因为回归直线方程一定过样本中心点，将样本点的中心（4，5）分别代入各个选项，只有C满足，故选C
考点：线性回归直线方程
点评：本题提供的两种方法，其实原理都是一样的，都是运用了样本中心点的坐标满足回归直线方程
名校课堂系列答案总体有编号为01,02,…,19,20的20个个体组成。利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为 （ ）
| 7816 6572 0802 6314 0702 4369 9728 0198 |
| 3204 9234 4935 8200 3623 4869 6938 7481 |
A．08 B．07 C．02 D．01
某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是( )
| A．y＝－10x＋200 | B．y＝10x＋200 |
| C．y＝－10x－200 | D．y＝10x－200 |
某日用品按行业质量标准分成五个等级，等级系数X依次为1，2，3，4，5．现从一批该种日用品中随机抽取200件，对其等级系数进行统计分析，得到频率
的分布表如下：
则在所取的200件日用品中，等级系数X=1的件数为
| A．40 | B．20 | C．30 | D．60 |
从甲乙两个城市分别随机抽取16台自动售货机，对其销售额进行统计，统计数据用茎叶图表示(如图所示)．设甲乙两组数据的平均数分别为
甲，乙，中位数分别为m甲，m乙，则( )．
| A．甲＜乙，m甲＞m乙 | B．甲＜乙，m甲＜m乙 |
| C．甲＞乙，m甲＞m乙 | D．甲＞乙，m甲＜m乙 |
已知某单位有职工120人，其中男职工90人。现在采用分层抽样（按男女分层）抽取一个样本，若样本中有3名女职工，则样本容量为（ ）。
| A．9 | B．12 | C．10 | D．15 |
为了了解某地区高三学生的身体素质情况，抽查了该地区
名年龄为17.5岁－18岁的男生体重(
) ,得到频率分布直方图如下
根据上图可得这名学生中体重在[56.5,64.5]的学生人数是（ ）
A． | B．30 | C． | D．50 |
如果数据
、
、……
的平均值为
，方差为
，则
，
，…… 
的平均值和方差分别为（ ）
| A．和 | B．3+5和9 |
| C．3+5和 | D．3+5 和9+30 +25 |
=bx+a必过（ ）
B．点
C．点
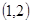D．点