题目内容
【题目】已知函数f（x）= 
（a＞0，且a≠1）在R上单调递减，且关于x的方程|f（x）|=2﹣x恰好有两个不相等的实数解，则a的取值范围是（ ）
A.（0， 
]
B.[ ， 
]
C.[ 
， ]∪{ }
D.[ ， ）∪{ }
【答案】C
【解析】解：y=loga（x+1）+1在[0，+∞）递减，则0＜a＜1，
函数f（x）在R上单调递减，则：
；
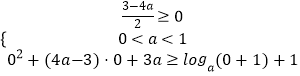解得， 
；
由图象可知，在[0，+∞）上，|f（x）|=2﹣x有且仅有一个解，
故在（﹣∞，0）上，|f（x）|=2﹣x同样有且仅有一个解，
当3a＞2即a＞ 
时，联立|x2+（4a﹣3）x+3a|=2﹣x，
则△=（4a﹣2）2﹣4（3a﹣2）=0，
解得a= 
或1（舍去），
当1≤3a≤2时，由图象可知，符合条件，
综上：a的取值范围为[ 
， ]∪{ }，
所以答案是：C．
练习册系列答案
阅读快车系列答案
相关题目
