题目内容
已知点集![]() ,其中
,其中![]() ,
,![]() ,点列
,点列![]() 在L中,
在L中,![]() 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列![]() 的公差为1,
的公差为1,![]() 。
。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() =
=![]() ,令
,令![]() ;试用解析式写出
;试用解析式写出![]() 关于
关于![]() 的函数。
的函数。
(3)若![]() =
=![]() ,给定常数m(
,给定常数m(![]() ),是否存在
),是否存在![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(1)![]() (2)
(2) (
(![]() )
)
(3)存在
解析:
(1)y=![]() ·
·![]() =(2x-b)+(b+1)=2x+1 -----(1分)
=(2x-b)+(b+1)=2x+1 -----(1分)
![]() 与
与![]() 轴的交点
轴的交点![]() 为
为![]() ,所以
,所以![]() ; -----(1分)
; -----(1分)
所以![]() ,即
,即![]() , -----(1分)
, -----(1分)
因为![]() 在
在![]() 上,所以
上,所以![]() ,即
,即![]() -----(1分)
-----(1分)
(2)设![]()
![]() (
(![]() ),
),
即![]()
![]() (
(![]() ) ----(1分)
) ----(1分)
(A)当![]() 时,
时,![]()
![]() ----(1分)
----(1分)
=![]() =
=![]() ,而
,而![]() ,所以
,所以![]() ----(1分)
----(1分)
(B)当![]() 时,
时,![]() ----(1分)
----(1分)
= ![]() =
=![]() , ----(1分)
, ----(1分)
而![]() ,所以
,所以![]() ----(1分)
----(1分)
因此 (
(![]() ) ----(1分)
) ----(1分)
(3)假设![]() ,使得
,使得![]() ,
,
(A)![]() 为奇数
为奇数
(一)![]() 为奇数,则
为奇数,则![]() 为偶数。则
为偶数。则![]() ,
,![]() 。则
。则![]() ,解得:
,解得:![]() 与
与![]() 矛盾。 ----(1分)
矛盾。 ----(1分)
(二)![]() 为偶数,则
为偶数,则![]() 为奇数。则
为奇数。则![]() ,
,![]() 。则
。则![]() ,解得:
,解得:![]() (
(![]() 是正偶数)。 ----(1分)
是正偶数)。 ----(1分)
(B)![]() 为偶数
为偶数
(一)![]() 为奇数,则
为奇数,则![]() 为奇数。则
为奇数。则![]() ,
,![]() 。则
。则![]() ,解得:
,解得:![]() (
(![]() 是正奇数)。 ----(1分)
是正奇数)。 ----(1分)
(二)![]() 为偶数,则
为偶数,则![]() 为偶数。则
为偶数。则![]() ,
,![]() 。则
。则![]() ,解得:
,解得:![]() 与
与![]() 矛盾。 ----(1分)
矛盾。 ----(1分)
由此得:对于给定常数m(![]() ),这样的
),这样的![]() 总存在;当
总存在;当![]() 是奇数时,
是奇数时,![]() ;当
;当![]() 是偶数时,
是偶数时,![]() 。 ----(1分)
。 ----(1分)

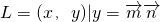 ,其中
,其中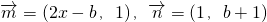 ,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,(n∈N+)
,点列Pn(an,bn)在L中,P1为L与y轴的交点,等差数列{an}的公差为1,(n∈N+)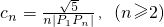 ,求
,求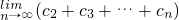
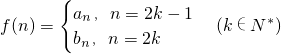 ,是否存在k∈N+,使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.
,是否存在k∈N+,使得f(k+11)=2f(k),若存在,求出k的值;若不存在,请说明理由.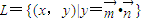 ,其中
,其中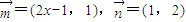 ,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.
,点列Pn(an,bn)在L中,P1为L与y轴的公共点,等差数列{an}的公差为1.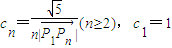 ,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.
,数列{cn}的前n项和Sn满足M+n2Sn≥6n对任意的n∈N*都成立,试求M的取值范围.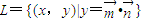 ,其中
,其中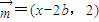 ,
,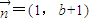 ,点Pn(an,bn)∈L,P1=L∩{(x,y)|x=1},且an+1-an=1,则数列{bn}的通项公式为 .
,点Pn(an,bn)∈L,P1=L∩{(x,y)|x=1},且an+1-an=1,则数列{bn}的通项公式为 .