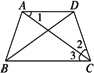
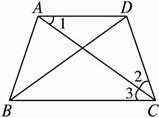
题目内容
在梯形ABCD中(图1),∠DAB=∠ABC=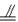
(Ⅰ)确定λ的值,并计算二面角D-BF-C的大小;
(Ⅱ)求点C到平面BDF的距离.
解:(1)EA、EB、EF两两垂直,以![]() 、
、![]() 、
、![]() 分别显x、y、z轴建立空间直角坐标系,
分别显x、y、z轴建立空间直角坐标系,
则E(0,0,0),B(4-4λ,4,0),C(4-4λ,4,0),C(4-4λ,2,0),
D(0,2,4λ),![]() =(4λ-4,2,0),
=(4λ-4,2,0),![]() =(4-4λ,2,0)
=(4-4λ,2,0)
∵![]() ⊥
⊥![]() ∴-(4λ-4)2+4=0
∴-(4λ-4)2+4=0![]() λ=
λ=![]() ;
;
即A(0,0,2),B(2,0,0),D(0,2,2),F(0,3,0)
![]() =(-2,3,0),
=(-2,3,0),![]() =(-2,2,2)
=(-2,2,2)
设平面DBF的一个法向量为n1=(x,y,z)
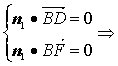 n1=(3,2,1)
n1=(3,2,1)
又平面BCF的一个法向n2=(0,0,1)
cos<n1,n2>=![]()
∴二面角D-BF-C的平面角为π-arccos![]()
(Ⅱ)∵C(2,4,0) ∴![]() =(0,4,0)
=(0,4,0)
∴点C到面BDF的距离为d=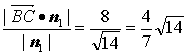
证法二:(Ⅰ)∵AE⊥BE,![]() =λ,∴EF∥AD,
=λ,∴EF∥AD,
∵AD⊥AE ∴EF⊥AE ∴AE⊥平而EBCF.
作DH⊥EF于H,则DH⊥平面EBCF. ∴DH![]() AE
AE
∵EG⊥BD ∴EG⊥BH.
∵BG=![]() BC=AD=EH ∴EBGH是矩形
BC=AD=EH ∴EBGH是矩形
对角线互相垂直的矩形是正方形
∴EB=BG=![]() AB.∴λ=
AB.∴λ=![]()
过H作HK⊥BF于K,连DK,则DK⊥BF
tan∠DKH=
∴∠DKH=arctan![]()
∴二画角D-BF-C为π-arctan![]()
(或π-arccos![]() )
)
(Ⅱ)VD-BFC=VC-BDF 设C到平面BDF的距离为d
S△BDF·d=S△BCF·DH![]() d=
d=![]()

练习册系列答案
相关题目