题目内容
用数学归纳法证明“
 ,
,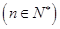 ”时,从“
”时,从“ ”到“
”到“ ”左边需要添加的代数式为( )
”左边需要添加的代数式为( )
A. | B. | C. | D. |
D
解析试题分析:解:当n=k时,左边等于(k+1)(k+2)…(k+k)=(k+1)(k+2)…(2k),
当n=k+1时,左边等于 (k+2)(k+3)…(k+k)(2k+1)(2k+2),
故从“k”到“k+1”的证明,左边需增添的代数式是  ,故选D.
,故选D.
考点:数学归纳法.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
数列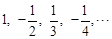 的一个通项公式为( )
的一个通项公式为( )
A.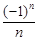 | B.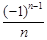 | C.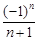 | D.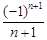 |
在数列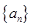 中,已知
中,已知 ,
, ,记
,记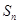 为数列
为数列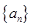 的前
的前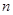 项和,则
项和,则 ( )
( )
A. | B. | C. | D. |
各项均为正数的数列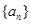 ,
,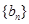 满足:
满足: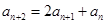 ,
,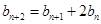 ,
,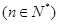 ,那么( )
,那么( )
A.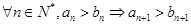 | B.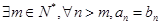 |
C.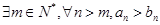 | D. |
已知数列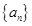 的前
的前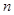 项和
项和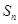 满足:
满足: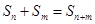 ,且
,且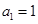 ,那么
,那么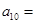 ( )
( )
| A.1 | B.9 | C.10 | D.55 |
已知数列{an}满足a1=1,a2=1,an+1=|an-an-1|(n≥2),则该数列前2011项的和S2011等于( )
| A.1341 | B.669 | C.1340 | D.1339 |
已知数列 满足
满足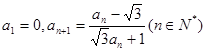 ,则
,则 等于( )
等于( )
A.0 | B.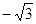 | C.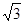 | D. |
已知数列{an}中,a1=1, =
= +3(n∈N*),则a10=( )
+3(n∈N*),则a10=( )
| A.28 | B.33 | C. | D. |