题目内容
函数f(x)=lg
的定义域为 ,其图象关于 对称.
| 1-x |
| 1+x |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据对数的定义真数大于0,求得函数的定义域,再根据函数的奇偶性的定义判断即可
解答:
解:∵函数f(x)=lg
,
∴
>0,
即-<x<1,
故函数的定义域为(-1,1);
∵f(-x)=lg
=-lg
=-f(x),
∴函数f(x)为奇函数,
故函数的图象关于原点对称.
故答案为:(-1,1),原点
| 1-x |
| 1+x |
∴
| 1-x |
| 1+x |
即-<x<1,
故函数的定义域为(-1,1);
∵f(-x)=lg
| 1+x |
| 1-x |
| 1-x |
| 1+x |
∴函数f(x)为奇函数,
故函数的图象关于原点对称.
故答案为:(-1,1),原点
点评:本题主要考查了对数函数的定义域,以及函数的奇偶性,属于基础题

练习册系列答案
相关题目
在抽查某批产品尺寸的过程中,样本尺寸数据的频率分布表如,则b等于( )
| 分组 | [100,200] | (200,300] | (300,400) | (400,500) | (500,600) | (600,700) |
| 频数 | 10 | 30 | 40 | 80 | 20 | m |
| 频率 | 0.05 | 0.15 | 0.2 | 0.4 | a | b |
| A、0.3 | B、0.25 |
| C、0.2 | D、0.1 |
设f(x)在x0处可导,
的值是( )
| lim |
| △x→0 |
| f(x0-2△x)-f(x0) |
| △x |
| A、2f′(x0) |
| B、-f′(x0) |
| C、-2f′(x0) |
| D、不一定存在 |
命题p:|x|<1,命题q:x2+x-6<0,则¬p是¬q成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
条件甲:复数z为纯虚数,条件乙:z+
=0,那么甲是乙的( )
. |
| z |
| A、必要非充分条件 |
| B、充分非必要条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
已知复数z=
,则z对应的点所在的象限是( )
| -2+4i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
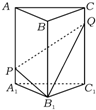 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为