题目内容
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱 ,
,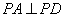 ,底面
,底面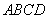 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 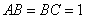 ,O为AD中点。
,O为AD中点。
(1)求直线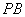 与平面
与平面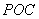 所成角的余弦值;
所成角的余弦值;
(2)求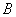 点到平面
点到平面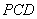 的距离;
的距离;
 (3)线段
(3)线段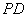 上是否存在一点
上是否存在一点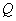 ,使得二面角
,使得二面角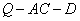 的余弦值为
的余弦值为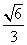 ?若存在,求出
?若存在,求出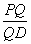 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1) 在△PAD中PA=PD, O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD, 平面 平面ABCD=AD,
平面ABCD=AD,  平面PAD,
平面PAD,
 所以PO⊥平面ABCD.
所以PO⊥平面ABCD.
又在直角梯形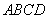 中,易得
中,易得 ;
;
所以以 为坐标原点,
为坐标原点, 为
为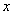 轴,
轴, 为
为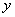 轴,
轴,
 为
为 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则 ,
, ,
,
 ,
, ;
;

 ,易证:
,易证: ,
,
所以 平面
平面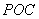 的法向量,
的法向量,

所以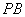 与平面
与平面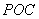 所成角的余弦值为
所成角的余弦值为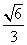 …………….4分
…………….4分
(2) ,设平面PDC的法向量为
,设平面PDC的法向量为 ,
,
则 ,取
,取 得
得
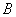 点到平面
点到平面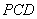 的距离
的距离 ……………….8分
……………….8分


练习册系列答案
相关题目
 ,若
,若 ,则
,则 _______
_______ 的方程
的方程
 (其中
(其中 是自然对数的底数)的有三个不
是自然对数的底数)的有三个不 的取值范围是
的取值范围是 } D. {
} D. { }
} 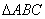 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )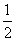 B、
B、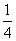 C、
C、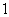 D、
D、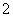
 ,若实数
,若实数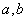 满足
满足 ,则
,则 ______
______ ,
, ,则向量
,则向量 在向量
在向量 方向上的投影为( )
方向上的投影为( ) B.
B.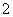 C.
C. D.
D.
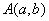 ,
,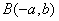 在函数
在函数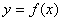 的图象上,则称
的图象上,则称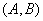 是函数
是函数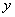 轴
轴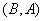 视为同一组), 则函数
视为同一组), 则函数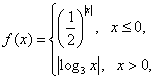 关于
关于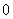 B.
B. C.
C.
 ,那么它的体积为
,那么它的体积为 B.
B. C.
C.  D.
D. 
 的共轭复数是
的共轭复数是 C.
C. D.
D. 