题目内容
已知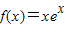 ,
,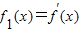 ,
,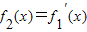 ,…
,…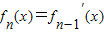 ,n∈N*
,n∈N*(1)请写出fn(x)的表达式(不需要证明);
(2)求fn(x)的极小值;
(3)设
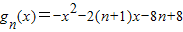 ,gn(x)的最大值为a,fn(x)的最小值为b,证明:a-b≥e-4.
,gn(x)的最大值为a,fn(x)的最小值为b,证明:a-b≥e-4.
【答案】分析:(1)由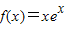 ,
,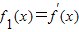 ,
,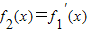 ,…
,…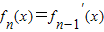 ,n∈N*,知f1(x)=ex+xex=(x+1)ex,
,n∈N*,知f1(x)=ex+xex=(x+1)ex,
f2(x)=ex+(x+1)ex=(x+2)ex,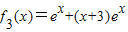 ,…,由此能求出fn(x)=(x+n)•ex,n∈N*
,…,由此能求出fn(x)=(x+n)•ex,n∈N*
(2)由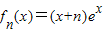 ,知
,知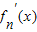 =(x+n+1)ex,由此能求出fn(x)的极小值.
=(x+n+1)ex,由此能求出fn(x)的极小值.
(3)由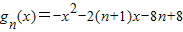 ,gn(x)的最大值为a,fn(x)的最小值为b,知a-b=(n-3)2+e-(n+1).令h(x)=(x-3)2+e-(x+1),(x≥0).由此能够证明a-b≥e-4.
,gn(x)的最大值为a,fn(x)的最小值为b,知a-b=(n-3)2+e-(n+1).令h(x)=(x-3)2+e-(x+1),(x≥0).由此能够证明a-b≥e-4.
解答:解:(1)∵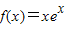 ,
,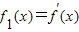 ,
,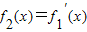 ,…
,…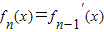 ,n∈N*
,n∈N*
∴f1(x)=ex+xex=(x+1)ex,
f2(x)=ex+(x+1)ex=(x+2)ex,
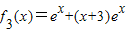 ,
,
…
∴fn(x)=(x+n)•ex,n∈N*
(2)∵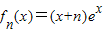 ,
,
∴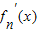 =(x+n+1)ex,
=(x+n+1)ex,
∵x>-(n+1)时,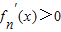 ;x<-(n+1)时,
;x<-(n+1)时,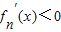 ,
,
∴当x=-(n+1)时,fn(x)取得极小值fn(-(n+1))=-e-(n+1).
(3)∵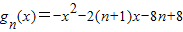 ,
,
gn(x)的最大值为a,fn(x)的最小值为b,
∴a=gn(-(n+1))=(n-3)2,b=fn(-(n+1))=-e-(n+1).
∴a-b=(n-3)2+e-(n+1).
令h(x)=(x-3)2+e-(x+1),(x≥0)
则h′(x)=2(x-3)-e-(x+1),
∵h′(x)在区间[0,+∞)上单调递增,
∴h′(x)≥h′(0)=-6-e-1,
∵h′(3)=-e-4<0,h′(4)=2-e-5>0,
∴存在x∈(3,4),使得h′(x)=0.
∴0≤x≤x时,h′(x)<0;当x>x时,h′(x)>0.
即h(x)在区间[x,+∞)上单调递增;在区间[0,x)音调递减,
∴h(x)min=h(x).
∵h′(3)=-e-4<0,h′(4)=2-e-5>0,
∴当n=3时,a-b取得最小值e-4,
所以a-b≥e-4.
点评:本题考查导数在求最大值、最小值中的应用,综合性强,难度大,有一定的探索性,对数学思想的要求较高.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
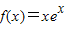 ,
,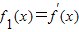 ,
,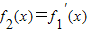 ,…
,…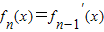 ,n∈N*,知f1(x)=ex+xex=(x+1)ex,
,n∈N*,知f1(x)=ex+xex=(x+1)ex,f2(x)=ex+(x+1)ex=(x+2)ex,
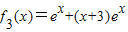 ,…,由此能求出fn(x)=(x+n)•ex,n∈N*
,…,由此能求出fn(x)=(x+n)•ex,n∈N*(2)由
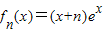 ,知
,知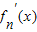 =(x+n+1)ex,由此能求出fn(x)的极小值.
=(x+n+1)ex,由此能求出fn(x)的极小值.(3)由
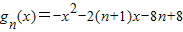 ,gn(x)的最大值为a,fn(x)的最小值为b,知a-b=(n-3)2+e-(n+1).令h(x)=(x-3)2+e-(x+1),(x≥0).由此能够证明a-b≥e-4.
,gn(x)的最大值为a,fn(x)的最小值为b,知a-b=(n-3)2+e-(n+1).令h(x)=(x-3)2+e-(x+1),(x≥0).由此能够证明a-b≥e-4.解答:解:(1)∵
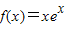 ,
,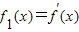 ,
,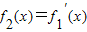 ,…
,…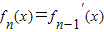 ,n∈N*
,n∈N*∴f1(x)=ex+xex=(x+1)ex,
f2(x)=ex+(x+1)ex=(x+2)ex,
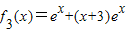 ,
,…
∴fn(x)=(x+n)•ex,n∈N*
(2)∵
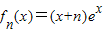 ,
,∴
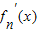 =(x+n+1)ex,
=(x+n+1)ex,∵x>-(n+1)时,
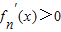 ;x<-(n+1)时,
;x<-(n+1)时,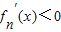 ,
,∴当x=-(n+1)时,fn(x)取得极小值fn(-(n+1))=-e-(n+1).
(3)∵
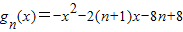 ,
,gn(x)的最大值为a,fn(x)的最小值为b,
∴a=gn(-(n+1))=(n-3)2,b=fn(-(n+1))=-e-(n+1).
∴a-b=(n-3)2+e-(n+1).
令h(x)=(x-3)2+e-(x+1),(x≥0)
则h′(x)=2(x-3)-e-(x+1),
∵h′(x)在区间[0,+∞)上单调递增,
∴h′(x)≥h′(0)=-6-e-1,
∵h′(3)=-e-4<0,h′(4)=2-e-5>0,
∴存在x∈(3,4),使得h′(x)=0.
∴0≤x≤x时,h′(x)<0;当x>x时,h′(x)>0.
即h(x)在区间[x,+∞)上单调递增;在区间[0,x)音调递减,
∴h(x)min=h(x).
∵h′(3)=-e-4<0,h′(4)=2-e-5>0,
∴当n=3时,a-b取得最小值e-4,
所以a-b≥e-4.
点评:本题考查导数在求最大值、最小值中的应用,综合性强,难度大,有一定的探索性,对数学思想的要求较高.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
