题目内容
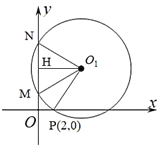
【题目】如图,已知动圆![]() 过点
过点![]() ,且在
,且在![]() 轴上截得弦
轴上截得弦![]() 的长为4.
的长为4.

(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() ,过点
,过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别与轨迹
分别与轨迹![]() 交于
交于![]() ,
,![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,试问
,试问![]() 是否为定值?若是,求出此定值;若不是,请说明理由.
是否为定值?若是,求出此定值;若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 为定值
为定值![]() ,理由见解析.
,理由见解析.
【解析】
(1)设动圆圆心坐标,利用弦心距,半弦长,半径所成的直角三角形列方程,化简可得;
(2)设A,B的坐标,AB的方程,与抛物线方程联立可得根与系数关系,当![]() 时,可得
时,可得![]() ;当
;当![]() 时,由A,F可得AC的方程,与抛物线方程联立可得A,C坐标的关系,同法得B,D坐标的关系,然后
时,由A,F可得AC的方程,与抛物线方程联立可得A,C坐标的关系,同法得B,D坐标的关系,然后![]() 用C,D坐标表示后可转化为A,B的坐标,从而得到
用C,D坐标表示后可转化为A,B的坐标,从而得到![]() 与
与![]() 的关系,得到定值.
的关系,得到定值.
(1)如图所示,设动圆的圆心![]() ,由题意,
,由题意,![]() ,
,
当![]() 不在
不在![]() 轴上时,过
轴上时,过![]() 作
作![]() 交
交![]() 于
于![]() ,则
,则![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,
,
∴![]() ,化简得
,化简得![]() ;
;
又当![]() 在
在![]() 轴上时,由已知可得
轴上时,由已知可得![]() 与
与![]() 重合,点
重合,点![]() 的坐标
的坐标![]() 也满足方程
也满足方程![]() ,
,
∴动圆圆心![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;
;
(2)![]() 为定值
为定值![]() ,下面给出证明:
,下面给出证明:
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
联立![]() 得
得![]() ,
,
∴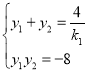 ,
,
①当![]() 时,
时,
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() :
:![]() ,
,![]() ,
,
∴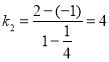 ,
,![]() .
.
若![]() ,同理可得
,同理可得![]() ;
;
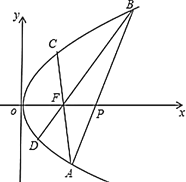
②当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,
,
联立 得
得![]() ,
,
则![]() ,故
,故![]() ,同理
,同理![]() ,
,
故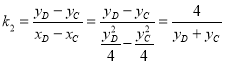
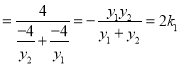 ,
,
∴![]() (定值).
(定值).
综上得![]() 为定值
为定值![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.

(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;
(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?
是否做操 是否近视 | 不做操 | 做操 |
近视 | 44 | 32 |
不近视 | 6 | 18 |
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中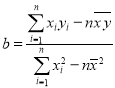 .
.
参考数据:![]() .
.
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附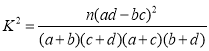 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |