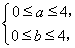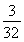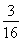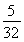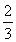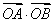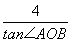题目内容
已知数列{2n－1·an}的前n项和Sn＝1－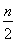
.
(1)求数列{an}的通项公式；
(2)设bn＝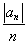
，求数列
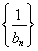的前n项和．
（1）
（2）(1－n)·2n＋1－2
【解析】(1)由题意可知：Sn－1＝1－
(n≥2)，
又2n－1·an＝Sn－Sn－1，∴2n－1·an＝－
.
∴an＝－
＝－2－n(n≥2)．∴a1＝－
.
又S1＝1－
＝
，∴a1≠S1，∴an＝
(2)由题意知bn＝
(n≥2)，∴
＝n·2n(n≥2)．
∵
＝
＝2，∴
＝n·2n(n≥1)．
设
的前n项和为
，则
＝1×2＋2×22＋3×23＋…＋n·2n，
2
＝1×22＋2×23＋3×24＋…＋(n－1)·2n＋n·2n＋1，
∴
－2
＝1×2＋22＋23＋…＋2n－n·2n＋1＝2＋22＋…＋2n－n·2n＋1，
∴－
＝(1－n)·2n＋1－2，∴
＝(n－1)·2n＋1＋2
练习册系列答案
相关题目
