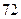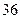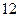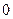题目内容
设函数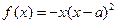 (
(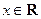 ),其中
),其中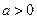 ,求函数
,求函数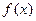 的极大值和极小值.
的极大值和极小值.
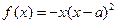 (
(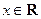 ),其中
),其中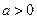 ,求函数
,求函数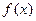 的极大值和极小值.
的极大值和极小值.函数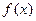 在
在 处取得极小值
处取得极小值 ,且
,且 ,函数
,函数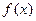 在
在 处取得极大值
处取得极大值 ,且
,且
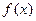 在
在 处取得极小值
处取得极小值 ,且
,且 ,函数
,函数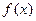 在
在 处取得极大值
处取得极大值 ,且
,且
先求驻点,再列表判断极值求出极值。 ,
,
 .
.
令 ,解得
,解得 或
或 .
.
由于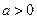 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表:
因此,函数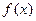 在
在 处取得极小值
处取得极小值 ,且
,且 ;
;
函数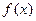 在
在 处取得极大值
处取得极大值 ,且
,且 .
.
【名师指引】求极值问题严格按解题步骤进行。
 ,
, .
.令
 ,解得
,解得 或
或 .
.由于
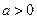 ,当
,当 变化时,
变化时, 的正负如下表:
的正负如下表: |  |  |  |  |  |
 |  |  |  |  |  |
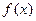 在
在 处取得极小值
处取得极小值 ,且
,且 ;
;函数
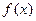 在
在 处取得极大值
处取得极大值 ,且
,且 .
.【名师指引】求极值问题严格按解题步骤进行。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
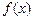 的定义域为
的定义域为 ,导函数
,导函数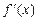 的图像如图所示,给出函数
的图像如图所示,给出函数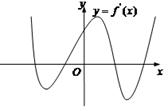
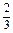 时,y=f(x)有极值.
时,y=f(x)有极值.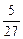
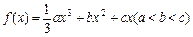 ,其图象在点
,其图象在点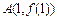 ,
,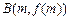 处的切线的斜率分别为
处的切线的斜率分别为
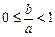 ;
; 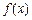 的递增区间为
的递增区间为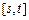 ,求|
,求|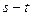 |的取值范围;
|的取值范围;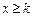 时(
时(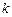 是与
是与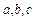 无关的常数),恒有
无关的常数),恒有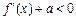 ,试求
,试求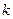 的最小值。
的最小值。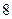 分为两个数,使其和为
分为两个数,使其和为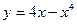 ,在
,在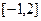 上的最大、最小值分别为( )
上的最大、最小值分别为( )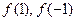
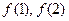
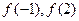
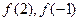
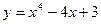 在区间
在区间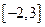 上的最小值为( )
上的最小值为( )