Question

如图1-19,已知四边形ABCD中,AC、BD交于点E,若∠BAC=∠BDC,求证:∠1=∠2.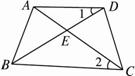

图1-19

Answer 1

思路分析:要证∠1=∠2,因为∠AED=∠BEC,?

所以,只要证△AED∽△BEC即可,考察条件∠BAC =∠BDC,容易得到△ABE∽△DCE,?

从而有=,即=.?

再由∠AED =∠BEC,△AED与△BEC相似便成为现实.

证明:在△ABE和△DCE中,∵∠BAC =∠BDC,∠AEB =∠DEC,?

∴△ABE∽△DCE.?

∴=,即=.?

在△AED和△BEC中,∵∠AED =∠BEC,?

∴△AED∽△BEC.?

∴∠ADE =∠BCE,即∠1=∠2.