题目内容
各项都为正数且公差不为零的等差数列a1,a2,a3,…,an,把离首末两项“距离”相等的两项之积排成数列,则该数列是 ( )
A.递减数列 B.递增数列
C.奇数项递增、偶数项递减的数列 D.先增后减的数列
思路分析:取满足已知条件的数列1,2,3,4,5,6.则按题目要求得到派生数列6,10,12,12,10,6. (*)
根据数列(*)特点便可排除A、B、C.那么选项D正确吗?数列(*)是先增后减的数列,递增递减也是有规律的.我们会想:对满足条件的任意等差数列是否都有此结论呢?我们研究下面的命题:
a1,a2,a3,…,an(n≥3)是公差不为零的等差数列,a1an,a2an-1,…,an
设等差数列{an}的公差为d,记数列a1an,a2an-1,…,an
∴bk+1-bk=ak+1an-k-akan-k+1
=(ak+d)(an-k+1-d)-akan-k+1
=(an-k+1-ak)d-d2.
①若n为奇数,当k<![]() 时,bk+1>bk;当k>
时,bk+1>bk;当k>![]() 时,bk+1<bk.
时,bk+1<bk.
∴b1<b2<…<![]() <
<![]() >
>![]() >…>bn.
>…>bn.
∴{bn}是一个先增后减的数列,并且中间项最大.
①若n为偶数,当k<![]() 时,bk+1>bk;当k=
时,bk+1>bk;当k=![]() 时,bk+1=bk;当k>
时,bk+1=bk;当k>![]() 时,bk+1<bk.
时,bk+1<bk.
∴b1<b2<…<![]() =
=![]() >
>![]() +2>…>bn.
+2>…>bn.
∴{bn}是一个先增后减的数列,并且中间两项相等且最大,都等于![]()
![]() .
.
综上证明知,a1an,a2an-1,…,an
答案:D


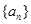 、
、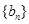 满足
满足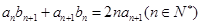 .
.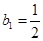 时,求数列
时,求数列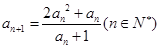 ,
,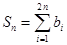 ,求证:
,求证: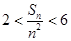 .
.