题目内容
【题目】棱长为2的正方体在平面![]() 上的射影的面积最大值等于________________.
上的射影的面积最大值等于________________.
【答案】![]()
【解析】
对正方体而言,无论从外部那个角度看,最多只能看到三个面,所以可只考虑共顶点的三个面在某一个平面上的射影的面积的最值就就足够了,正方体共顶点在平面![]() 上的射影的面积记为
上的射影的面积记为![]() ,这三个平面与平面
,这三个平面与平面![]() 所成二面角分别记为
所成二面角分别记为![]() ,则
,则
![]() ,可证
,可证![]() ,利用基本不等式,可求出
,利用基本不等式,可求出![]() 的最大值,即可得出结论.
的最大值,即可得出结论.
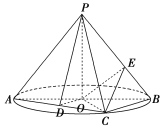
先推导一个结论:
三棱锥![]() 的三条侧棱
的三条侧棱![]() 两两互相垂直,
两两互相垂直,
三侧面与底面所成的二面角分别记为![]() ,则有
,则有
![]() 成立,以下证明:
成立,以下证明:
如图,![]() 是
是![]() 在底面
在底面![]() 上的射影,
上的射影,
连![]() 并延长分别交三边于
并延长分别交三边于![]() ,
,
连![]() ,
,![]() 两两互相垂直,
两两互相垂直,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 是二面角
是二面角![]() 的平面角,记为
的平面角,记为![]() ,
,
同理另两侧面与底面所成二面角分别为![]()
记为![]() ,三侧面
,三侧面![]() 及底面
及底面![]() 的面积分别记为
的面积分别记为
![]() 平面
平面![]() ,
,![]() (射影面积公式),
(射影面积公式),
同理![]() ,①
,①
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,②
,②
①代入②,![]() ;
;
正方体的边长为2,每个面的面积为4,
正方体共顶点在平面![]() 上的射影的面积记为
上的射影的面积记为![]() ,
,
这三个平面与平面![]() 所成二面角分别记为
所成二面角分别记为![]() ,则
,则
![]() ,
,
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() ,等号成立,
,等号成立,
正方体在平面![]() 上的射影是如下图所示的正六边形,其面积最大为
上的射影是如下图所示的正六边形,其面积最大为![]() .
.
故答案为:![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目