题目内容
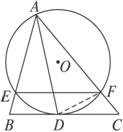
如图2-4-6,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,弦BD∥XY,AC、BD相交于点E.（1）求证:△ABE≌△ACD;
（2）若AB =6 cm,BC=4 cm,求AE的长.
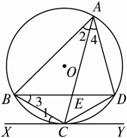
图2-4-6
思路解析:第（1）问中的全等已经具备了AB =AC,再利用弦切角定理与圆周角定理可以得角的相等关系;对于（2）,则利用△BCE∽△ACB建立比例式,解方程获得AE的长.
（1）证明:∵XY是⊙O的切线,∴∠1=∠2.?
∵BD∥XY,∴∠1=∠3.?
∴∠2=∠3.?
∵∠3=∠4,∴∠2=∠4.?
∵∠ABD =∠ACD,?
又∵AB =AC,?
∴△ABE≌△ACD.
（2）解:∵∠3 =∠2,∠BCE =∠ACB,?
∴△BCE∽△ACB.?
∴
=
.?
∴AC·CE = BC2,?
即AC·(AC-AE )=BC2.?
∵AB =AC =6,BC =4,?
∴6(6-AE )=16.?
∴
.
练习册系列答案
相关题目
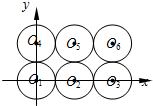如图，有6个半径都为1的圆，其圆心分别为O1（0，0），O2（2，0），O3（4，0），O4（0，2），O5（2，2），O6（4，2）．记集合M={⊙Oi|i=1，2，3，4，5，6}．若A，B为M的非空子集，且A中的任何一个圆与B中的任何一个圆均无公共点，则称 （A，B） 为一个“有序集合对”（当A≠B时，（A，B） 和 （B，A） 为不同的有序集合对），那么M中“有序集合对”（A，B） 的个数是（ ）
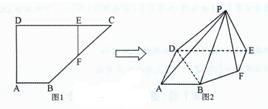如图1，在直角梯形ABCD中，AB∥CD，∠A=90°，AB=2，CD=6，AD=3，E为CD上一点，且DE=4，过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF，使∠PED=60°，如图2．
的图象如图所示，则
的值一定