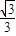题目内容
计算cos(
分析:构造三个向量a=(sinα,cosα),b=(sin(![]() π+α),cos(
π+α),cos(![]() π+α)),c=(sin(
π+α)),c=(sin(![]() π+α),cos(
π+α),cos(![]() π+α)),利用a,b,c之间的关系求解.
π+α)),利用a,b,c之间的关系求解.
解:令a=(sinα,cosα),b=(sin(![]() π+α),cos(
π+α),cos(![]() π+α)),
π+α)),
c=(sin(![]() π+α),cos(
π+α),cos(![]() π+α)).
π+α)).
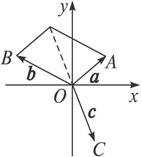
如图所示,|a|=|b|=|c|=1,cos∠AOB=![]() =sinαsin(
=sinαsin(![]() π+α)+cosαcos(
π+α)+cosαcos(![]() π+
π+
α)=cos![]() π,同理,cos∠BOC=cos∠COA=cos
π,同理,cos∠BOC=cos∠COA=cos![]() π.由向量加法的几何意义得a+b=-c.所以a+b+c=0,
π.由向量加法的几何意义得a+b=-c.所以a+b+c=0,
即cosα+cos(![]() +α)+cos(
+α)+cos(![]() +α)=0.
+α)=0.
点评:本题的计算利用了平面向量的数量积、向量加法的平行四边形法则,体现了数形结合的思想.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
计算cos 28° cos17°-sin 28° sin17°的结果等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
计算cos(-600°)的结果是( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|