题目内容
已知椭圆C: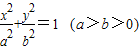 的离心率为
的离心率为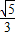 ,定点M(2,0),椭圆短轴的端点是B1,B2,且MB1⊥MB2.
,定点M(2,0),椭圆短轴的端点是B1,B2,且MB1⊥MB2.(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点M且斜率不为0的直线交椭圆C于A,B两点.试问x轴上是否存在定点P,使PM平分∠APB?若存在,求出点P的坐标;若不存在,说明理由.
【答案】分析:(Ⅰ)利用离心率为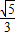 ,可得
,可得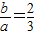 ,由椭圆短轴的端点是B1,B2,且MB1⊥MB2,可得△MB1B2是等腰直角三角形,由此可求椭圆C的方程;
,由椭圆短轴的端点是B1,B2,且MB1⊥MB2,可得△MB1B2是等腰直角三角形,由此可求椭圆C的方程;
(Ⅱ)设线AB的方程与椭圆C的方程联立,利用韦达定理,结合PF平分∠APB,则直线PA,PB的倾斜角互补,建立方程,即可求得结论.
解答:解:(Ⅰ)由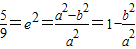 ,得
,得 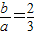 .…(2分)
.…(2分)
依题意△MB1B2是等腰直角三角形,从而b=2,故a=3.…(4分)
所以椭圆C的方程是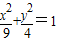 .…(5分)
.…(5分)
(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为x=my+2.
将直线AB的方程与椭圆C的方程联立,消去x得 (4m2+9)y2+16my-20=0.…(7分)
所以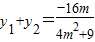 ,
,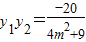 .…(8分)
.…(8分)
若PF平分∠APB,则直线PA,PB的倾斜角互补,所以kPA+kPB=0.…(9分)
设P(a,0),则有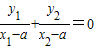 .
.
将 x1=my1+2,x2=my2+2代入上式,整理得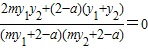 ,
,
所以 2my1y2+(2-a)(y1+y2)=0.…(12分)
将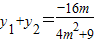 ,
,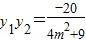 代入上式,整理得 (-2a+9)•m=0.…(13分)
代入上式,整理得 (-2a+9)•m=0.…(13分)
由于上式对任意实数m都成立,所以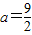 .
.
综上,存在定点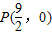 ,使PM平分∠APB.…(14分)
,使PM平分∠APB.…(14分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查存在性问题的探究,属于中档题.
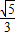 ,可得
,可得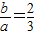 ,由椭圆短轴的端点是B1,B2,且MB1⊥MB2,可得△MB1B2是等腰直角三角形,由此可求椭圆C的方程;
,由椭圆短轴的端点是B1,B2,且MB1⊥MB2,可得△MB1B2是等腰直角三角形,由此可求椭圆C的方程;(Ⅱ)设线AB的方程与椭圆C的方程联立,利用韦达定理,结合PF平分∠APB,则直线PA,PB的倾斜角互补,建立方程,即可求得结论.
解答:解:(Ⅰ)由
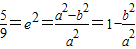 ,得
,得 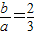 .…(2分)
.…(2分)依题意△MB1B2是等腰直角三角形,从而b=2,故a=3.…(4分)
所以椭圆C的方程是
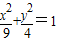 .…(5分)
.…(5分)(Ⅱ)设A(x1,y1),B(x2,y2),直线AB的方程为x=my+2.
将直线AB的方程与椭圆C的方程联立,消去x得 (4m2+9)y2+16my-20=0.…(7分)
所以
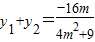 ,
,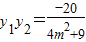 .…(8分)
.…(8分)若PF平分∠APB,则直线PA,PB的倾斜角互补,所以kPA+kPB=0.…(9分)
设P(a,0),则有
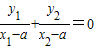 .
.将 x1=my1+2,x2=my2+2代入上式,整理得
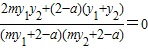 ,
,所以 2my1y2+(2-a)(y1+y2)=0.…(12分)
将
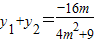 ,
,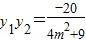 代入上式,整理得 (-2a+9)•m=0.…(13分)
代入上式,整理得 (-2a+9)•m=0.…(13分)由于上式对任意实数m都成立,所以
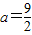 .
.综上,存在定点
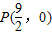 ,使PM平分∠APB.…(14分)
,使PM平分∠APB.…(14分)点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查存在性问题的探究,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、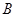 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.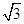
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线