题目内容
(2013•青岛二模)已知点F(1,0)为椭圆C:
+
=1(a>b>0)的右焦点,过点A(a,0)、B(0,b)的直线与圆x2+y2=
相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 过点F的直线交椭圆C于M、N两点,求证:
+
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| 12 |
| 7 |
(Ⅰ)求椭圆C的方程;
(Ⅱ) 过点F的直线交椭圆C于M、N两点,求证:
| 1 |
| |MF| |
| 1 |
| |NF| |
分析:(Ⅰ)由焦点坐标知c=1,则a2=b2+1①,写出直线AB方程并化简,由直线与圆相切得d2=
=
②,联立①②解得a,b即得椭圆C的方程;
(Ⅱ)设M(x1,y1)、N(x2,y2),分情况讨论:(1)当直线l的斜率不存在时,x1=x2=1,易求
+
的值;(2)当直线l的斜率存在时,设l:y=k(x-1),代入椭圆方程消掉y得x的二次方程,利用两点间距离公式可把|MF|、|NF|用横坐标表示出来,不妨设x2<1,x1>1,则
+
通分后可代入韦达定理,化简即得数值,综合(1)(2)即得结论;
| (ab)2 |
| a2+b2 |
| 12 |
| 7 |
(Ⅱ)设M(x1,y1)、N(x2,y2),分情况讨论:(1)当直线l的斜率不存在时,x1=x2=1,易求
| 1 |
| |MF| |
| 1 |
| |NF| |
| 1 |
| |MF| |
| 1 |
| |NF| |
解答:解:(Ⅰ)因为F(1,0)为椭圆的右焦点,所以a2=b2+1①,
AB的直线方程为
+
=1,即bx+ay-ab=0,
所以d2=
=
,化简得12(a2+b2)=7a2b2②,
由①②得:a2=4,b2=3,
所以椭圆C的方程为
+
=1;
(Ⅱ) 设M(x1,y1)、N(x2,y2),
(1)当直线l的斜率不存在时,x1=x2=1,则
+
=1,解得y12=
,
所以|MF|=|NF|=
,则
+
=
;
(2)当直线l的斜率存在时,设l:y=k(x-1),
联立
,得(3+4k2)x2-8k2x+4k2-12=0,
则x1+x2=
,x1x2=
,
|MF|=
=
=
|x1-1|,
同理|NF|=
|x2-1|,
不妨设x2<1,x1>1,则
+
=
(
+
)
=
(
+
)=
×
=
×
=
×
=
,
综(1)(2),所以
+
为定值
.
AB的直线方程为
| x |
| a |
| y |
| b |
所以d2=
| (ab)2 |
| a2+b2 |
| 12 |
| 7 |
由①②得:a2=4,b2=3,
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ) 设M(x1,y1)、N(x2,y2),
(1)当直线l的斜率不存在时,x1=x2=1,则
| 1 |
| 4 |
| y12 |
| 3 |
| 9 |
| 4 |
所以|MF|=|NF|=
| 3 |
| 2 |
| 1 |
| |MF| |
| 1 |
| |NF| |
| 4 |
| 3 |
(2)当直线l的斜率存在时,设l:y=k(x-1),
联立
|
则x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
|MF|=
| (x1-1)2+y12 |
| (x1-1)2+k2(x1-1)2 |
| 1+k2 |
同理|NF|=
| 1+k2 |
不妨设x2<1,x1>1,则
| 1 |
| |MF| |
| 1 |
| |NF| |
| 1 | ||
|
| 1 |
| |x2-1| |
| 1 |
| |x1-1| |
=
| 1 | ||
|
| 1 |
| 1-x2 |
| 1 |
| x1-1 |
| 1 | ||
|
| ||
| x1+x2-x1x2-1 |
=
| 1 | ||
|
| ||||||
|
| 1 | ||
|
12
| ||
| 9 |
| 4 |
| 3 |
综(1)(2),所以
| 1 |
| |MF| |
| 1 |
| |NF| |
| 4 |
| 3 |
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,弦长公式、韦达定理是解决该类题目常用知识,要熟练掌握,解决(Ⅱ)问的关键是设x2<1,x1>1去掉绝对值符号然后代入韦达定理.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=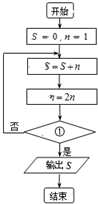 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )