题目内容
((本小题满分14分)
在数列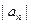 ,
,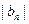 中,a1=2,b1=4,且
中,a1=2,b1=4,且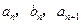 成等差数列,
成等差数列,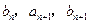 成等比数列(
成等比数列(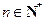 )
)
(Ⅰ)求a2,a3,a4及b 2,b3,b4,由此猜测
2,b3,b4,由此猜测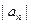 ,
,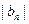 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)证明: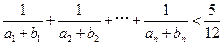 .
.
在数列
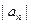 ,
,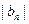 中,a1=2,b1=4,且
中,a1=2,b1=4,且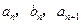 成等差数列,
成等差数列,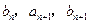 成等比数列(
成等比数列(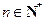 )
)(Ⅰ)求a2,a3,a4及b
 2,b3,b4,由此猜测
2,b3,b4,由此猜测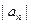 ,
,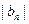 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;(Ⅱ)证明:
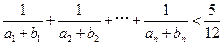 .
.由条件得
由此 可得
可得
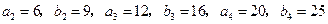 .································ 2分
.································ 2分
猜测 .································································ 4分
.································································ 4分
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
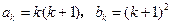 ,
,
那么当n=k+1时,
 .
.
所以当n=k+1时,结论也成立.
由①②,可知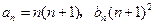 对一切正整数都成立.······························· 7分
对一切正整数都成立.······························· 7分
(Ⅱ)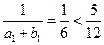 .
.
n≥2时,由(Ⅰ)知 .·································· 9分
.·································· 9分
故


综上,原不等式成立. ············································································ 14分

由此
 可得
可得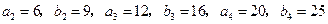 .································ 2分
.································ 2分猜测
 .································································ 4分
.································································ 4分用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
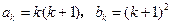 ,
,那么当n=k+1时,
 .
.所以当n=k+1时,结论也成立.
由①②,可知
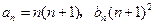 对一切正整数都成立.······························· 7分
对一切正整数都成立.······························· 7分(Ⅱ)
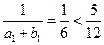 .
.n≥2时,由(Ⅰ)知
 .·································· 9分
.·································· 9分故



综上,原不等式成立. ············································································ 14分
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
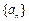 是公差为
是公差为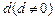 的等差数列,
的等差数列,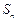 为其前
为其前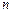 项和。
项和。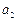 ,
,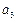 ,
,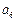 依次成等比数列,求其公比
依次成等比数列,求其公比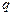 ;
;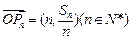 ,求证:对任意的
,求证:对任意的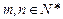 ,向量
,向量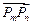 与向量
与向量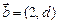 共线;
共线;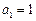 ,
,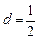 ,
,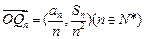 ,问是否存在一个半径最小的圆,使得对任意的
,问是否存在一个半径最小的圆,使得对任意的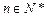 ,点
,点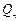 都在这个圆内或圆周上。
都在这个圆内或圆周上。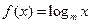 (
(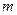 为常数,
为常数,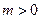 且
且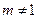 ),设
),设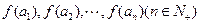 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列. 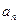 }是等比数列;
}是等比数列;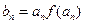 ,记数列
,记数列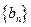 的前n项和为
的前n项和为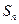 ,当
,当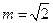 时,求
时,求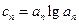 ,问是否存在实数
,问是否存在实数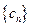 中每一项恒小于它后面的项?
中每一项恒小于它后面的项? 的前
的前 项和是
项和是 ,满足
,满足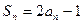 .
. 及前
及前 满足
满足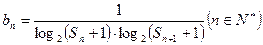 ,求数列
,求数列 ;
; ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 为等差数列,且a5=14,a7=20。
为等差数列,且a5=14,a7=20。 的通项公式;
的通项公式;
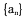 的前n项和为
的前n项和为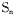 .若,
.若,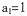
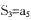 ,
,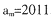 .则m=
.则m=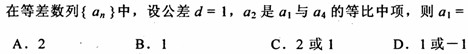
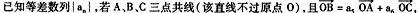

 的前n项和为
的前n项和为 ,若
,若 ,则当n=__________时,
,则当n=__________时,