题目内容
(本小题满分12分)某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为 .
.

(1)分别求出 ,
, 的值;
的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差 和
和 ,并由此分析两组技工的加工水平;
,并由此分析两组技工的加工水平;
(3)质检部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,若两人
加工的合格零件个数之和大于 ,则称该车间“质量合格”,求该车间“质量合格”的概率.
,则称该车间“质量合格”,求该车间“质量合格”的概率.
(注:方差 ,其中
,其中 为数据
为数据 的平均数).
的平均数).
(1) ,
, ;
;
(2) ,
, ,甲乙两组的整体水平相当,乙组更稳定一些;
,甲乙两组的整体水平相当,乙组更稳定一些;
(3) .
.
【解析】
试题分析:(1)根据茎叶图以及条件平均数都为 ,即可求得
,即可求得 ,
, ;(2)由(1)求得的数据以及条件中注的方差计算公式即可求得甲乙两组的方差,再由平均数以及方差的统计意义,可知平均数相表示甲乙两组的整体水平相当,再由甲的方差大于乙的方差可知甲的方差可知乙组更稳定一些;(3)分析题意可知问题适合用古典概型分析,穷举总共的基本事件共有
;(2)由(1)求得的数据以及条件中注的方差计算公式即可求得甲乙两组的方差,再由平均数以及方差的统计意义,可知平均数相表示甲乙两组的整体水平相当,再由甲的方差大于乙的方差可知甲的方差可知乙组更稳定一些;(3)分析题意可知问题适合用古典概型分析,穷举总共的基本事件共有 个,而符合题意的基本事件共有
个,而符合题意的基本事件共有 个,因此所求概率为
个,因此所求概率为 .
.
试题解析:(1)根据题意可得: ,∴
,∴ ,
, ,∴
,∴ ;(2)根据题意可得:
;(2)根据题意可得: ,
,
 ,
,
∵ ,
, ,∴甲乙两组的整体水平相当,乙组更稳定一些;
,∴甲乙两组的整体水平相当,乙组更稳定一些;
(3)质监部门从该车间甲、乙两组技工中各随机抽取一名技工,对其加工的零件进行检测,设两人加工的合格零件数分别为 ,则所有的
,则所有的 有
有 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,共计
,共计 个,而
个,而 的基本事件有
的基本事件有 ,
, ,
, ,
, ,
, ,共计
,共计 个基本事件,故满足
个基本事件,故满足 的基本事件共有
的基本事件共有 ,即该车间“待整改”的基本事件有
,即该车间“待整改”的基本事件有 个,故该车间“待整改”的概率为
个,故该车间“待整改”的概率为 .
.
考点:1.茎叶图;2.方差与标准差;(3)古典概型求概率.

练习册系列答案
相关题目
 的图象如图,则( )
的图象如图,则( )




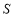 值是 ()
值是 ()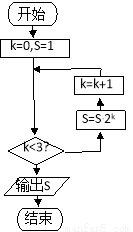
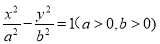 的左右焦点为
的左右焦点为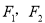 ,
,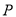 是双曲线右支上一点,满足条件
是双曲线右支上一点,满足条件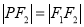 ,直线
,直线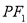 与圆
与圆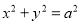 相切,则双曲线的离心率为( )
相切,则双曲线的离心率为( )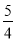 (B)
(B)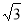 (C)
(C)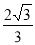 (D)
(D)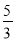
 的图象( )
的图象( ) 轴对称 (B)关于
轴对称 (B)关于 轴对称
轴对称 对称
对称 ,若函数
,若函数 有三个不同的零点,则实数
有三个不同的零点,则实数 的取值范围是 .
的取值范围是 . 与圆
与圆 有两个不同交点的一个充分不必要条件是( )
有两个不同交点的一个充分不必要条件是( ) B.
B. C.
C. D.
D.
 对定义域
对定义域 内的任意
内的任意 都有
都有 ,且当
,且当 时,其导函数
时,其导函数
 ,若
,若 ,则( )
,则( )



 ,集合
,集合 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.