题目内容
6.在△ABC中,若AB=5,AC=12,|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$的值为$\frac{25}{13}$.分析 如图所示,设$\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow{AD}$,又|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,可得平行四边形ABDC是矩形.利用直角三角形的边角关系即可得出.
解答 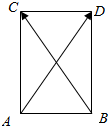 解:如图所示,设$\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow{AD}$,
解:如图所示,设$\overrightarrow{AB}+\overrightarrow{AC}$=$\overrightarrow{AD}$,
∴四边形ABDC是平行四边形.
∵|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,
∴平行四边形ABDC是矩形.
∴|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
在Rt△ABC中,cos∠ABC=$\frac{5}{13}$.
则$\frac{\overrightarrow{BA}•\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\frac{5×13×\frac{5}{13}}{13}$=$\frac{25}{13}$.
故答案为:$\frac{25}{13}$.
点评 本题考查了向量的平行四边形法则、矩形的定义、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设α为锐角,则“tanα>2”是“-$\frac{4}{3}$<tan2α<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.若sin(π+α)=-$\frac{1}{2}$,则sin(4π-α)的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.已知sinβ=$\frac{1}{3}$,cos(α+β)=-1,则sin(α+2β)的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
15.已知数列{an}满足an+1=an-2(n∈N+),他的前n项的和为Sn,则Sn的最大值是S3是a1=5的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |