题目内容
17.已知 f(x)=$\frac{1}{4}$x2+sin($\frac{5π}{2}$+x),f′(x)为f(x)的导函数,则 y=f′(x)的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据题意,对函数f(x)求导可得其导数的解析式,由其解析式分析可得f′(x)=$\frac{1}{2}$x-sinx为奇函数,且有3个零点,分析选项即可得答案.
解答 解:根据题意,f(x)=$\frac{1}{4}$x2+sin($\frac{5π}{2}$+x)=$\frac{1}{4}$x2+cosx,
其导数f′(x)=$\frac{1}{2}$x-sinx,
分析可得:f′(-x)=$\frac{1}{2}$(-x)-sin(-x)=-($\frac{1}{2}$x-sinx)=-f′(x),
且函数y=$\frac{1}{2}$x与y=sinx的图象有3个交点,
即f′(x)=$\frac{1}{2}$x-sinx为奇函数,且有3个零点,
分析选项可得A符合;
故选:A.
点评 本题考查函数的导数与单调性的关系,涉及函数的导数的计算,关键是正确求出函数f(x)的导数.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
5.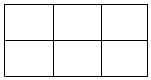 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )| A. | 208 | B. | 204 | C. | 200 | D. | 196 |
2.随着移动互联网时代的到来,手机的使用非常普遍,“低头族”随处可见.某校为了解家长和教师对学生带手机进校园的态度,随机调查了100位家长和教师,得到情况如下表:
(1)是否有95%以上的把握认为“带手机进校园与身份有关”,并说明理由;
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 教师 | 家长 | |
| 反对 | 40 | 20 |
| 支持 | 20 | 20 |
(2)把以上频率当概率,随机抽取3位教师,记其中反对学生带手机进校园的人数为X,求随机变量X的分布列和数学期望.
附:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
9.在△ABC中,A,B,C所对的边长分别为a,b,c,且满足$cosA=\frac{3}{5}$,$\overrightarrow{AB}•\overrightarrow{AC}=3$,则△ABC的面积为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | 3 | D. | 5 |
6.设实数x,y满足$\left\{\begin{array}{l}{x-2y+7≤0}\\{x+y-5≥0}\\{2x-y-4≥0}\end{array}\right.$,则z=x+2y的最值情况正确的是( )
| A. | 最小值为7,最大值为17 | B. | 最小值为9,最大值为17 | ||
| C. | 最小值为17,无最大值 | D. | 最大值为17,无最小值 |

 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.