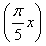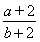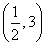题目内容
设函数f(x)=x2+aln(x+1)有两个极值点x1,x2,且x1<x2.
(1)求实数a的取值范围;
(2)当a= 时,判断方程f(x)=-
时,判断方程f(x)=- 的实数根的个数,并说明理由.
的实数根的个数,并说明理由.
(1)0<a< (2)方程f(x)=-
(2)方程f(x)=- 有且只有一个实数根
有且只有一个实数根
【解析】(1)由f(x)=x2+aln(x+1),可得f′(x)=2x+ (x>-1).
(x>-1).
令g(x)=2x2+2x+a(x>-1),则其对称轴为x=- .由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为
.由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为 解得0<a<
解得0<a<  .
.
(2)由a= 可知x1=-
可知x1=- ,x2=-
,x2=- ,从而易知函数y=f(x)在
,从而易知函数y=f(x)在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
①由y=f(x)在 上单调递增,且f
上单调递增,且f =
= +
+ ·ln
·ln =
= -
- ln 2>-
ln 2>- ,以及f
,以及f =
= +
+ ·ln
·ln =-
=- -
- +
+ <-
<- ,故方程f(x)=-
,故方程f(x)=- 在
在 有且只有一个实根;
有且只有一个实根;
②由于y=f(x)在 上单调递减,在
上单调递减,在 上单调递增,因此f(x)在
上单调递增,因此f(x)在 上的最小值f
上的最小值f =
= +
+ ·ln
·ln =
= +
+ ln
ln >-
>- ,故方程f(x)=-
,故方程f(x)=- 在
在 上没有实数根.
上没有实数根.
综上可知,方程f(x)=- 有且只有一个实数根
有且只有一个实数根

公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
X | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,+∞) |
人数 | t | 1 | 1 | 1 | 1 | 1 |
依据上述材料回答下列问题:
(1)求t的值;
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率.