如图.在直三棱柱ABC -A1B1C1 中.AB = AC = 1.AA1 = .AB⊥AC 求异面直线BC1与AC所成角的度数题目和参考答案——青夏教育精英家教网——

题目内容

如图，在直三棱柱ABC —A₁B₁C₁中，AB = AC = 1，AA₁= 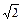，AB⊥AC 求异面直线BC₁与AC所成角的度数

解：在直三棱柱ABC—A₁B₁C₁中，AC // A₁C₁，∴∠B C₁A₁就是BC₁
与AC所成的角 …2分连结A₁B，在△A₁B C₁中，由已知得BA₁=，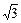
A₁C₁=1，BC₁="2" ，…2分由余弦定理得cos∠BC₁A₁= ，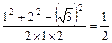
∴∠B C₁A₁=60°，…3分因此直线BC₁与AC所成的角为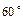

解析

练习册系列答案

今日课堂课时作业系列答案

金版卷王课程探究大试卷系列答案

金榜之路系列答案

金点中考系列答案

金海全A突破系列答案

金考卷45套汇编系列答案

全景文化中考试题汇编3年真题2年模拟系列答案

金牌教练赢在燕赵系列答案

0系列答案

金题金卷热点测试系列答案

相关题目

如图，在直三棱柱AB-A₁B₁C₁中．∠ BAC=90°，AB=AC=AA₁ =1．D是棱CC₁上的一P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA．

(I)求证：CD=C₁D：

(II)求二面角A-A₁D-B的平面角的余弦值；　

(Ⅲ)求点C到平面B₁DP的距离．

(本小题共l2分)

如图，在直三棱柱AB-A₁B₁C₁中．∠ BAC=90°，AB=AC=AA₁ =1．D是棱CC₁上的一[来源:]

P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA．

(I)求证：CD=C₁D：

(II)求二面角A-A₁D-B的平面角的余弦值；

(Ⅲ)求点C到平面B₁DP的距离．

(本小题共l2分)

如图，在直三棱柱AB-A₁B₁C₁中．∠ BAC=90°，AB=AC=AA₁ =1．D是棱CC₁上的一

P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA．

(I)求证：CD=C₁D：

(II)求二面角A-A₁D-B的平面角的余弦值；

(Ⅲ)求点C到平面B₁DP的距离．

如图，在直三棱柱AB-A₁B₁C₁中，∠ BAC=90°，AB=AC=AA₁=1，D是棱CC₁上一点，P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA。

（I）求证：CD=C₁D；
（II）求二面角A-A₁D-B的平面角的余弦值；
（Ⅲ）求点C到平面B₁DP的距离

如图，在直三棱柱AB-A₁B₁C₁中．∠ BAC=90°，AB=AC=AA₁ =1．D是棱CC₁上的一点，P是AD的延长线与A₁C₁的延长线的交点，且PB₁∥平面BDA．

(I)求证：CD=C₁D：

(II)求二面角A-A₁D-B的平面角的余弦值；

(Ⅲ)求点C到平面B₁DP的距离．