Question

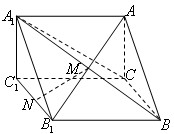如图，在直三棱柱ABC-A₁B₁C₁中，AC⊥BC，且AC=BC=CC₁=2，M是AB₁，A₁B的交点，N是B₁C₁的中点．
（Ⅰ）求证：MN⊥平面A₁BC；
（Ⅱ）求平面AA₁B与平面A₁BC夹角的大小．

Answer 1

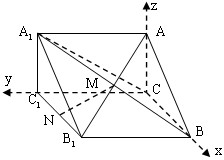（Ⅰ）证明：以C为原点，分别以CB、CC₁、CA为x、y、z轴建立坐标系，则由AC=BC=CC₁=2，知A₁（0，2，2），B₁（2，2，0），B（2，0，0），C₁（0，2，0），∴M（1，1，1），N（1，2，0），
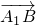∴=（2．-2，-2），=（2，0，0），=（0，1，-1），…（3分）
∴，，
∴MN⊥A₁B，MN⊥CB，∴MN⊥平面A₁BC； …（6分）
（Ⅱ）作CH⊥AB于H点，∵平面ABC⊥平面ABB₁A₁，∴CH⊥平面A₁BA，
故平面A₁BA的一个法向量为，
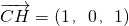而平面A₁BC的一个法向量为，…（9分）
∴cos=||=
∵，
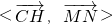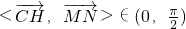∴平面AA₁B与平面A₁BC夹角的大小为．…（12分）
分析：（Ⅰ）以C为原点，分别以CB、CC₁、CA为x、y、z轴建立坐标系，用坐标表示点与向量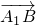、、，可得MN⊥A₁B，MN⊥CB，从而可得MN⊥平面A₁BC；
（Ⅱ）作CH⊥AB于H点，则平面A₁BA的一个法向量为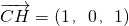，平面A₁BC的一个法向量为，利用向量的夹角公式，即可求得平面AA₁B与平面A₁BC夹角．
点评：本题考查线面垂直，考查面面角，考查利用空间向量解决立体几何问题，正确求出平面的法向量是关键．