题目内容
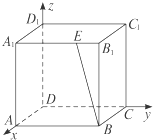
如图,在空间直角坐标系中,正方体ABCDA1B1C1D1的棱长为1,B1E=
A1B1,则
等于( )
| 1 |
| 4 |
| BE |

A、(0,
| ||
B、(-
| ||
C、(0,-
| ||
D、(
|
分析:利用正方体ABCDA1B1C1D1的棱长为1,B1E=
A1B1,可得点B,E的坐标,进而得到向量
.
| 1 |
| 4 |
| BE |
解答:解:∵正方体ABCDA1B1C1D1的棱长为1,B1E=
A1B1,
∴B(1,1,0),E(1,
,1),
∴
=(1,
,1)-(1,1,0)=(0,-
,1).
故选:C.
| 1 |
| 4 |
∴B(1,1,0),E(1,
| 3 |
| 4 |
∴
| BE |
| 3 |
| 4 |
| 1 |
| 4 |
故选:C.
点评:本题考查了正方体的性质、空间直角坐标系、向量的坐标运算,属于基础题.

练习册系列答案
相关题目
 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC, (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
 且
且

