题目内容

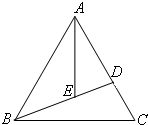精英家教网在△ABC中，
AD
=2
DC
，E是BD上的一点，若
AE
=x
AB
+
2
7
AC
，则实数x的值为
（　　）
A、
2
7
B、
3
7
C、
4
7
D、
5
7
分析：由向量的三角形法则可得：
AE
=
AB
+
BE
，由向量共线定理可设
BE
=t
BD
，而
BD
=
AD
-
AB
，
AD
=
2
3
AC
，代入并已知
AE
=x
AB
+
2
7
AC
比较即可解得x．
解答：解：由向量的三角形法则可得：
AE
=
AB
+
BE
，
设
BE
=t
BD
，而
BD
=
AD
-
AB
，
AD
=
2
3
AC
，
∴
AE
=
.
AB
+t(
2
3
AC
-
AB
)=(1-t)
AB
+
2
3
t
AC
，
而
AE
=x
AB
+
2
7
AC
，∴
1-t=x
2
3
t=
2
7
，解得x=
4
7
．
故选：C．
点评：本题考查了向量的三角形法则、向量共线定理、平面向量基本定理，属于基础题．
练习册系列答案
相关题目
精英家教网如图，在△ABC中，AD⊥AB，BCsinB=
3
，|
AD
|=1，则
AC
•
AD
=（　　）
A、2
3
B、
3
2
C、
3
3
D、
3
精英家教网如图，在△ABC中，AD⊥AB，
BC
=
3
BD
，|
AD
|=1，则
AC
•
AD
=
 
．
如图，在△ABC中，AD⊥BC，
AD
=
1
5
AB
+
4
5
AC
．
（1）求
|
CD
|
|
DB
|
的值；
（2）设cosC=
5
5
，且实数t满足|
CB
-t
CA
|≥|
AB
+
AC
|，求t的取值范围．
已知：在△ABC中，AD为∠BAC的平分线，AD的垂直平分线EF与AD交于点E，与BC的延长线交于点F，若CF=4，BC=5，则DF=
6
6
．
（2007广州市水平测试）在△ABC中，
AD
=
1
4
AB 
， E为BC边的中点，设
AB
=
a
，
AC
=
b
，则
DE
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网