题目内容
在数列{an}在中,an=4n-
,a1+a2+…an=an2+bn,n∈N*,其中a,b为常数,则
的值是______.
| 5 |
| 2 |
| lim |
| n→∞ |
| an-bn |
| an+bn |
∵an=4n-
,
∴a1=
,从而Sn=
=2n2-
.
∴a=2,b=-
,则
=1.
答案:1.
| 5 |
| 2 |
∴a1=
| 3 |
| 2 |
n(
| ||||
| 2 |
| n |
| 2 |
∴a=2,b=-
| 1 |
| 2 |
| lim |
| n→∞ |
2n-(-
| ||
2n+(-
|
答案:1.

练习册系列答案
相关题目
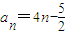 ,a1+a2+…an=an2+bn,n∈N*,其中a,b为常数,则
,a1+a2+…an=an2+bn,n∈N*,其中a,b为常数,则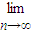
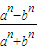 的值是 .
的值是 .