题目内容
【题目】已知![]() ,
,![]() 为抛物线
为抛物线![]() 上的相异两点,且
上的相异两点,且![]() .
.

(1)若直线![]() 过
过![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 的垂直平分线交
的垂直平分线交![]() 轴与点
轴与点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,联立抛物线方程,运用韦达定理和中点坐标公式,以及弦长公式,计算可得所求值;
,联立抛物线方程,运用韦达定理和中点坐标公式,以及弦长公式,计算可得所求值;
(2)设线段![]() 的中点为
的中点为![]() ,
,![]() ,运用中点坐标公式和直线的斜率公式,以及直线方程,可得
,运用中点坐标公式和直线的斜率公式,以及直线方程,可得![]() 的坐标,
的坐标,
设出直线![]() 的方程代入抛物线方程,运用韦达定理,以及弦长公式和点到直线的距离公式,化简整理,结合基本不等式可得所求最大值.
的方程代入抛物线方程,运用韦达定理,以及弦长公式和点到直线的距离公式,化简整理,结合基本不等式可得所求最大值.
解:(1)当垂直于![]() 轴或斜率为零时,显然不符合题意,所以可设直线
轴或斜率为零时,显然不符合题意,所以可设直线![]() 的方程为
的方程为![]() ,
,
代入方程![]() ,得
,得![]()
故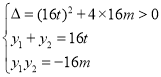
![]() ,
,
结合![]() 解得
解得![]() .
.
因此,![]() .
.
(2)设线段![]() 的中点为
的中点为![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,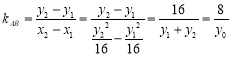 .
.
线段![]() 的垂直平分线的方程是
的垂直平分线的方程是![]() ,①
,①
由题意知![]() ,
,![]() 是①的一个解,
是①的一个解,
所以线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点
轴的交点![]() 为定点,
为定点,
且点![]() 坐标为
坐标为![]() .
.
直线![]() 的方程为
的方程为![]() ,
,
即![]() ,②
,②
②代入![]() 得
得![]() ,即
,即![]() ,③
,③
依题意,![]() ,
,![]() 是方程③的两个实根,且
是方程③的两个实根,且![]() ,
,
所以△![]() ,即
,即![]() .
.![]() ,
,![]() ,
,
![]()
![]() ,
,
点![]() 到线段
到线段![]() 的距离
的距离![]() ,
,
![]() .
.
当且仅当![]() ,即
,即![]() 时,上式取得等号.
时,上式取得等号.
所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某高校调查喜欢“统计”课程是否与性别有关,随机抽取了55个学生,得到统计数据如表:
喜欢 | 不喜欢 | 总计 | |
男生 | 20 | ||
女生 | 20 | ||
总计 | 30 | 55 |
(1)完成表格的数据;
(2)判断是否在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关?
参考公式:![]()
| 0.025 | 0.01 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |