题目内容
假设n=k时成立，当n=k+1时，证明1+
+
+
+…+
＞
(n∈N+)，左端增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| n |
| 2 |
| A．1项 | B．k-1项 | C．k项 | D．2k项 |
n=k时，不等式的左边等于 1+
+
+
+…+
，且 k∈N+，
当n=k+1时，不等式的左边等于 1+
+
+
+…+
+(
+
+
+…+
)，
当n=k+1时，不等式的左边比n=k时增加的向为
+
+
+…+
，共增加了 2k 项．
故选D．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
当n=k+1时，不等式的左边等于 1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| 2k+2k-1 |
当n=k+1时，不等式的左边比n=k时增加的向为
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+2 |
| 1 |
| 2k+2k-1 |
故选D．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
证明1+
+
+
+…+
＞
（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| n |
| 2 |
| A、1项 |
| B、k-1项 |
| C、k项 |
| D、2k项 |
+…+
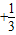
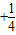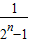
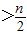（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（ ）
+…+
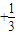
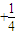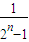
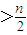（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（ ）