题目内容
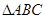 中,角
中,角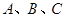 所对的边分别为
所对的边分别为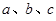 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).①若
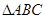 最小内角为
最小内角为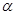 ,则
,则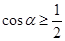 ;
;②若
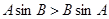 ,则
,则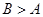 ;
;③存在某钝角
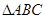 ,有
,有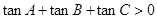 ;
;④若
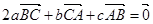 ,则
,则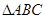 的最小角小于
的最小角小于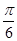 ;
;⑤若
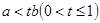 ,则
,则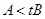 .
.①④⑤
对①,因为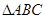 最小内角为
最小内角为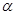 ,所以
,所以 ,
, ,故正确;对②,构造函数
,故正确;对②,构造函数 ,求导得,
,求导得, ,当
,当 时,
时, ,即
,即 ,则
,则 ,所以
,所以 ,即
,即 在
在 上单减,由②
上单减,由② 得
得 ,即
,即 ,所以
,所以 ,故②不正确;对③,因为
,故②不正确;对③,因为 ,则在钝角
,则在钝角 中,不妨设
中,不妨设 为钝角,有
为钝角,有 ,故
,故
③不正确;对④,由

 ,即
,即 ,而
,而 不共线,则
不共线,则 ,解得
,解得 ,则
,则 是最小的边,故
是最小的边,故 是最小的角,根据余弦定理
是最小的角,根据余弦定理 ,知
,知 ,故④正确;对⑤,由
,故④正确;对⑤,由 得
得 ,所以
,所以 ,由②知,
,由②知, ,即
,即 ,又根据正弦定理知
,又根据正弦定理知 ,即
,即 ,所以
,所以 ,即
,即 .故①④⑤正确.
.故①④⑤正确.
【考点定位】本题考查三角函数与解三角形、利用导数求函数的最值、不等式的应用等知识 ,意在考查 学生综合解题能力.
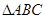 最小内角为
最小内角为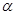 ,所以
,所以 ,
, ,故正确;对②,构造函数
,故正确;对②,构造函数 ,求导得,
,求导得, ,当
,当 时,
时, ,即
,即 ,则
,则 ,所以
,所以 ,即
,即 在
在 上单减,由②
上单减,由② 得
得 ,即
,即 ,所以
,所以 ,故②不正确;对③,因为
,故②不正确;对③,因为 ,则在钝角
,则在钝角 中,不妨设
中,不妨设 为钝角,有
为钝角,有 ,故
,故
③不正确;对④,由


 ,即
,即 ,而
,而 不共线,则
不共线,则 ,解得
,解得 ,则
,则 是最小的边,故
是最小的边,故 是最小的角,根据余弦定理
是最小的角,根据余弦定理 ,知
,知 ,故④正确;对⑤,由
,故④正确;对⑤,由 得
得 ,所以
,所以 ,由②知,
,由②知, ,即
,即 ,又根据正弦定理知
,又根据正弦定理知 ,即
,即 ,所以
,所以 ,即
,即 .故①④⑤正确.
.故①④⑤正确.【考点定位】本题考查三角函数与解三角形、利用导数求函数的最值、不等式的应用等知识 ,意在考查 学生综合解题能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的圆形(
的圆形( 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点 在圆弧上,点
在圆弧上,点 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设 与矩形材料的边
与矩形材料的边 的夹角为
的夹角为 ,圆柱的体积为
,圆柱的体积为
 .
.
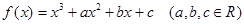 ,若函数
,若函数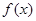 在区间
在区间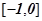 上是单调减函数,则
上是单调减函数,则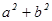 的最小值为
的最小值为
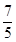


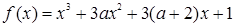 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数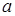 的取值范围是 。
的取值范围是 。 是( )
是( )
