题目内容
设函数，
（1）当
，解不等式，
；
（2）若
的解集为
，
，求证：
（1）
；（2）见解析
【解析】
试题分析：（1）由已知可得，原不等式可化为
等价于
或
或
解得
或
或
原不等式的解集为
5分
（2）依题可知
，所以
，即
7分
9分
当且仅当
，
,即
时取等号 10分
考点：本题考查基本不等式和绝对值不等式解法
点评：（1）当
时，不等式变形为
，利用零点分段法去绝对值号，解不等式即可；（2）利用
的解集为
求参数
的值，得
，则
，利用基本不等式求
的最小值即可．
练习册系列答案
相关题目
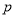：实数m满足
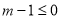，命题
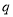：函数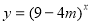
是增函数。若
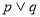为真命题，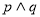
为假命题，则实数m的取值范围为（ ）
则
的值为（ ）
B．4 C．2 D．
及直线
截圆C所得的弦长均为10，则圆C的面积是 ．
中，D，E分别是AB，
的中点
；
，求三棱锥
的体积
的前
项和为
，已知
，则
的最小值为（ ）
B．
C．
D．
、
，设
为坐标原点，点
的坐标为
，记
．
的最大值，并求事件“
取得最大值”的概率；
的前
项和为
，且
中，令
， 
，求
．