题目内容
设函数f(x)=x+![]() (a>0).
(a>0).
(1)求函数在(0,+∞)上的单调区间,并证明之;
(2)若函数f(x)在[a-2,+∞]上递增,求a的取值范围.
答案:
解析:
解析:
|
(1)f(x)在(0,+∞)上的增区间为[ 证明:∵ ∴ 即f(x)在[ (2)[a-2,+∞]为[ 所以a-2≥ |

练习册系列答案
相关题目
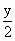 )是函数y=g(x)图象上的点.
)是函数y=g(x)图象上的点. ,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.
,D是由x轴和曲线y=f(x)及该曲线在点(1,0)处的切线所围成的封闭区域,则z=x-2y在D上的最大值为________.