Question

（2012•红桥区一模）一个三棱柱ABC-A₁B₁C₁．其正视图、俯视图均为矩形，正视图长为2

3

，宽为

3

，侧视图是正三角形，直观图如图所示，E为BC中点．
（Ⅰ）求三棱柱ABC-A₁B₁C₁的体积；
（Ⅱ）求证：A₁C∥平面AEB₁；
（Ⅲ）求BB₁与平面AEB₁所成角的正弦值．

Answer 1

分析：（I）根据正三棱柱的性质和三视图中的数据，算出底面边长为a=2且高为2

3

，由此即可算出三棱柱ABC-A₁B₁C₁的体积；
（II）连结A₁B交AB₁于点O，连结EO．利用三角形中位线定理和线面平行判定定理，即可证出A₁C∥平面AEB₁；
（III）设设B到平面AEB₁的距离为d，根据三棱锥B₁-ABE的体积等于三棱锥B-AEB₁的体积，算出三棱锥B₁-ABE的体积为1且S △AEB1=

39

2

，利用等体积转换得出B到平面AEB₁的距离d=

2 39

13

，由此利用线面所成角的定义与性质，即可算出BB₁与平面AEB₁所成角的正弦值等于

13

13

．

解答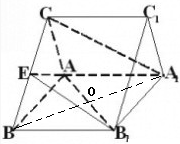：解：（I）根据题意，可得
∵正视图长为2

3

，宽为

3

，侧视图是正三角形，
∴三棱柱ABC-A₁B₁C₁的高为2

3

设底面边长为a，满足

3

2

a=

3

，解得a=2
因此，三棱柱ABC-A₁B₁C₁的体积V=S_△ABC•AA₁=

3

4

×2²×（2

3

）=6；
（II）连结A₁B交AB₁于点O，连结EO
∵E为BC中点，O为A₁B中点
∴EO是△A₁BC的中位线，可得EO∥A₁C
∵EO?平面AEB₁，A₁C?平面AEB₁
∴A₁C∥平面AEB₁；
（III）设B到平面AEB₁的距离为d
∵三棱锥B₁-ABE的体积为V₁=

1

3

×

1

2

×S_△ABC•BB₁=

1

6

×

3

×2

3

=1
∴三棱锥B-AEB₁的体积为

1

3

S △AEB1•d=1
∵AE=

3

2

AB=

3

，B₁E=

BE2+BB12

=

13

，AB₁=

AB2+BB12

=4
∴AE²+B₁E²=AB₁²，得△AEB₁是以E为直角顶点的直角三角形
得S △AEB1=

1

2

AE•B₁E=

39

2

因此，B到平面AEB₁的距离d=

1

1 3 S△AEB1

=

2 39

13

设BB₁与平面AEB₁所成角为α，则sinα=

d

BB1

=

13

13

即BB₁与平面AEB₁所成角的正弦值等于

13

13

．

点评：本题在正三棱柱中证明线面平行、并求线面角的正弦值和三棱柱的体积，着重考查了正三棱柱的性质、线面平行判定定理和直线与平面所成角的求法等知识，属于中档题．