题目内容
已知 的三内角
的三内角 、
、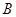 、
、 所对的边分别是
所对的边分别是 ,
, ,
, ,且
,且 ,
, ,
, 成等比数列。
成等比数列。
(1)若 ,求
,求 的值;
的值;
(2)求角B的最大值,并判断此时 的形状
的形状
(1) (2)B的最大值为
(2)B的最大值为 ,此时△ABC为等边三角形
,此时△ABC为等边三角形
解析试题分析:(1) ,再利用等比数列
,再利用等比数列 以及余弦定理即可求出cosB的值.
以及余弦定理即可求出cosB的值.
(2)由 ,
, ,
, 成等比数列,
成等比数列, ,由余弦定理可得
,由余弦定理可得 ,再由
,再由 在区间
在区间 上的单调性,
上的单调性, ,可知△ABC为等边三角形
,可知△ABC为等边三角形
(1)由 利用正弦定理化简得:
利用正弦定理化简得: ,又
,又 ,
, ,
, 成等比数列,
成等比数列, ,由余弦定理可得
,由余弦定理可得
(2) ,
,
∵函数 在区间
在区间 上为减函数,
上为减函数, ,即角B的最大值为
,即角B的最大值为 ,此时有
,此时有 ,且
,且 ,可得
,可得
则△ABC为等边三角形
考点:余弦定理的应用,等比数列的基本性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.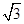 ,c=5,求b.
,c=5,求b. 两地连线上的定点
两地连线上的定点 处建造广告牌
处建造广告牌 ,其中
,其中 为顶端,
为顶端, 长35米,
长35米, 长80米,设
长80米,设 和
和 看
看 .
.
 ,问
,问 求
求 =
= .
. 的值;
的值; 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
.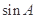 的值;
的值; ,
, ,求向量
,求向量 在
在 方向上的投影.
方向上的投影. +2sin2
+2sin2 =1,试判断△ABC的形状.
=1,试判断△ABC的形状. 分别为角A、B、C所对的边,且
分别为角A、B、C所对的边,且 .
. ,且
,且
 ,求
,求 的值.
的值. 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,若
,若 .
. ;
; ,
, 时,求
时,求 中,角
中,角 所对的边为
所对的边为 ,且满足
,且满足
 的值;
的值; 且
且 ,求
,求 的取值范围.
的取值范围.