题目内容
已知-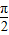
＜x＜0，则sinx+cosx=
．（I）求sinx-cosx的值；
（Ⅱ）求
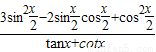的值．
【答案】分析：（Ⅰ）把sinx+cosx=
两边平方求得sinxcosx的值，进而根据∵（sinx-cosx）2=1-2sinxcosx求得（sinx-cosx）2=，进而根据-
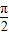＜x＜0确定sinx-cosx的正负，求得答案．
（Ⅱ）先把原式中的正切转换成弦，进而根据倍角公式化简整理，把（1）中求得的sinxcosx和sinx-cosx代入即可得到答案．
解答：解：（Ⅰ）由sinx+cosx=
，平方得sin2x+2sinxcosx+cos2x=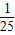
，
即2sinxcosx=-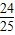
．
∵（sinx-cosx）2=1-2sinxcosx=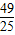
．
又∵-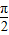
＜x＜0，∴sinx＜0，cosx＞0，sinx-cosx＜0，
故sinx-cos=-
．
（Ⅱ）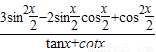
=
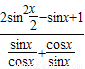=sinxcosx（2-cosx-sinx）
=（-
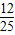）×（2-
）=-
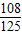
点评：本题主要考查了同角三角函数基本关系的应用．要特别注意函数值的正负号的判定．
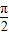两边平方求得sinxcosx的值，进而根据∵（sinx-cosx）2=1-2sinxcosx求得（sinx-cosx）2=，进而根据-＜x＜0确定sinx-cosx的正负，求得答案．（Ⅱ）先把原式中的正切转换成弦，进而根据倍角公式化简整理，把（1）中求得的sinxcosx和sinx-cosx代入即可得到答案．
解答：解：（Ⅰ）由sinx+cosx=
，平方得sin2x+2sinxcosx+cos2x=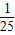，即2sinxcosx=-
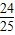．∵（sinx-cosx）2=1-2sinxcosx=
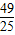．又∵-
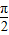＜x＜0，∴sinx＜0，cosx＞0，sinx-cosx＜0，故sinx-cos=-
．（Ⅱ）
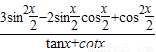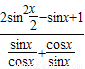==sinxcosx（2-cosx-sinx）=（-
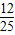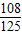
）×（2-）=-点评：本题主要考查了同角三角函数基本关系的应用．要特别注意函数值的正负号的判定．
练习册系列答案
相关题目
已知集合S={x|log2（x+1）＞0}，T={x|
＜0}，则S∩T等于（ ）
| 2-x |
| 2+x |
| A、（0，2） |
| B、（-1，2） |
| C、（-1，+∞） |
| D、（2，+∞） |
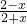＜0}，则S∩T等于
＜0}，则S∩T等于（ ）