题目内容
已知两点F1(-2,0),F2(2,0),曲线C上的动点M满足|MF1|+|MF2|=2|F1F2|,直线MF2与曲线C交于另一点P.
(Ⅰ)求曲线C的方程;
(Ⅱ)设N(-4,0),若 =3:2,求直线MN的方程.
=3:2,求直线MN的方程.
解:(Ⅰ)因为|F1F2|=4,|MF1|+|MF2|=2|F1F2|=8>4,
所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.
曲线C的方程为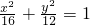 .(4分)
.(4分)
(Ⅱ)显然直线MN不垂直于x轴,也不与x轴重合或平行.(5分)
设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.
由 得(3+4k2)y2-24ky=0.
得(3+4k2)y2-24ky=0.
解得y=0或 .
.
依题意 ,
, .(7分)
.(7分)
因为 ,
,
所以 ,则
,则 .
.
于是
所以 (9分)
(9分)
因为点P在椭圆上,所以 .
.
整理得48k4+8k2-21=0,
解得 或
或 (舍去),
(舍去),
从而 .((11分))
.((11分))
所以直线MN的方程为 .(12分)
.(12分)
分析:(Ⅰ)由题意知|MF1|+|MF2|=2|F1F2|=8>4,所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.由此可知曲线C的方程;
(Ⅱ)设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.由 得(3+4k2)y2-24ky=0.解得y=0或
得(3+4k2)y2-24ky=0.解得y=0或 .依题意
.依题意 ,
, ;由此可知直线MN的方程.
;由此可知直线MN的方程.
点评:本题考查圆锥曲线的位置关系,解题时要认真审题,仔细解题.
所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.
曲线C的方程为
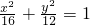 .(4分)
.(4分)(Ⅱ)显然直线MN不垂直于x轴,也不与x轴重合或平行.(5分)
设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.
由
 得(3+4k2)y2-24ky=0.
得(3+4k2)y2-24ky=0.解得y=0或
 .
.依题意
 ,
, .(7分)
.(7分)因为
 ,
,所以
 ,则
,则 .
.于是

所以
 (9分)
(9分)因为点P在椭圆上,所以
 .
.整理得48k4+8k2-21=0,
解得
 或
或 (舍去),
(舍去),从而
 .((11分))
.((11分))所以直线MN的方程为
 .(12分)
.(12分)分析:(Ⅰ)由题意知|MF1|+|MF2|=2|F1F2|=8>4,所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.由此可知曲线C的方程;
(Ⅱ)设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.由
 得(3+4k2)y2-24ky=0.解得y=0或
得(3+4k2)y2-24ky=0.解得y=0或 .依题意
.依题意 ,
, ;由此可知直线MN的方程.
;由此可知直线MN的方程.点评:本题考查圆锥曲线的位置关系,解题时要认真审题,仔细解题.

练习册系列答案
相关题目
 .
.