题目内容
(本题满分10分) 在长方体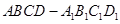 中,
中,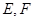 分别是
分别是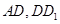 的中点,
的中点,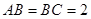 ,
,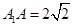 .
.
(Ⅰ)求证: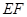 //平面
//平面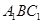 ;
;
(Ⅱ)在线段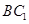 上是否存在点
上是否存在点 ,使直线
,使直线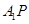 与
与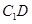 垂直,
垂直,
如果存在,求线段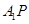 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.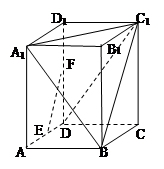
(Ⅰ)见解析;(Ⅱ) .
.
解析试题分析:(1)根据已知中的长方体的性质,结合线线平行,得到线面平行的证明。
(2)由于根据已知条件可知线A1D1垂直于平面CD1,进而利用性质定理得到线线垂直,相似来求解长度。
解:(Ⅰ)连接 ,在长方体
,在长方体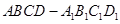 中,
中, ,则四边形
,则四边形 是平行四边形,∴
是平行四边形,∴ ,又∵
,又∵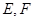 分别是
分别是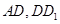 的中点∴
的中点∴ ,∴
,∴ ,又
,又 面
面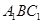 ,
, 面
面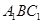 ,
,
∴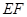 //平面
//平面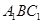 (3分)
(3分)
(Ⅱ)在平面 中作
中作 交
交 于
于 ,过
,过 作
作 交
交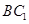 于点
于点 ,连
,连 ∵
∵

而
 又
又
 ∵
∵

 ∽
∽




 为直角梯形,且高
为直角梯形,且高
 .(10分)
.(10分)
考点:本题主要是考查线面平行的判定以及线线垂直的证明运用。
点评:解决该试题的关键是熟练的利用线面平行的判定定理,得到线线平行进而得到证明,同时线面的垂直,结合相似得到求解。

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
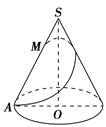
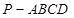 的侧面
的侧面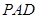 垂直于底面
垂直于底面 ,
,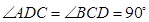
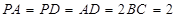 ,
,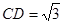 ,
, 在棱
在棱 上,
上,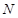 是
是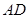 的中点,二面角
的中点,二面角 为
为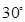 求
求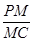 的值;
的值;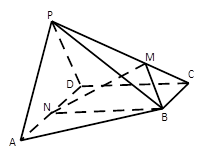
 中,
中, ,
,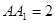 ,
,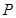 为
为 的中点。
的中点。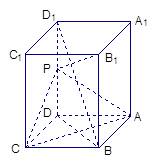
 ∥平面
∥平面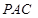 ;
; 平面
平面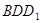 ;
;
 为梯形,
为梯形, ,
,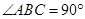 ,求图中阴影部分绕
,求图中阴影部分绕 旋转一周所形成的几何体的表面积和体积。
旋转一周所形成的几何体的表面积和体积。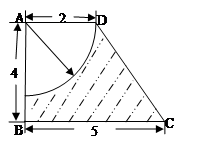
 时,有DN ∥平面AEM,求
时,有DN ∥平面AEM,求  的值;
的值;
 中, E是
中, E是 的中点.
的中点. 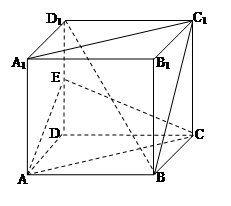
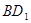 ∥平面AEC;
∥平面AEC;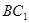 与平面
与平面 所成的角.
所成的角.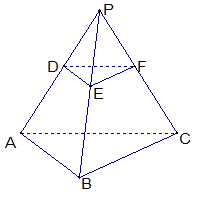
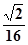 , 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
, 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.