题目内容
已知a，b是正数，求证（a+
）（2b+
）≥
．
证明：因为a，b是正数，利用均值不等式，
（a+）（2b+）=2ab+
+2+
=（2ab+）+
≥2+=，
所以（a+）（2b+）≥．
分析：把不等式左边利用多项式的乘法法则计算后，由a与b为正数，利用均值不等式a+b≥2
，当且仅当a=b时取等号，即可求出左边式子的最小值为，得证．
点评：此题考查了基本不等式的运用，是一道证明题．熟练掌握基本不等式是证明的关键．
（a+
）（2b+）=2ab++2+ =（2ab+
）+≥2+=，所以（a+
）（2b+）≥．分析：把不等式左边利用多项式的乘法法则计算后，由a与b为正数，利用均值不等式a+b≥2
，当且仅当a=b时取等号，即可求出左边式子的最小值为，得证．点评：此题考查了基本不等式的运用，是一道证明题．熟练掌握基本不等式是证明的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．解答应写出文字说明、证明过程或演算步骤．
选做题在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．
选做题在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．
]所对应的变换把直线l：2x-y=3变换为自身，求a，b的值．
t为参数）化为普通方程．
把圆C：x2+y2=1变换为椭圆E：
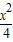
=1．
求实数a的值．
≥4．