题目内容
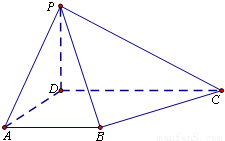
已知四棱锥P-ABCD的底面为直角梯形，∠BAD=∠ADC=90°，AB=AD=PD=1，PD⊥底面ABCD，平面PBC⊥平面PBD．（1）求证：CD=2；
（2）求平面PAD与平面PBC所成的锐二面角的大小．
【答案】分析：（1）作DE⊥PB于E，由平面PBC⊥平面PBD，得DE⊥BC，进而可得BC⊥BD．由AB=AD=1，AB∥CD，知∠CDB=∠DBA=45°，即可得到结论；
（2）延长DA，CB交于G，连接PG，作DH⊥PG于H，连接CH，则可得∠CHD是侧面PAD与侧面PBC所成二面角的平面角，由此能求出侧面PAD与侧面PBC所成锐二面角的大小．
解答：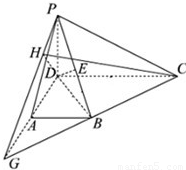
（1）证明：作DE⊥PB于E，
∵平面PBC⊥平面PBD，∴DE⊥平面PBC，∴DE⊥BC．
∵PD⊥BC，PD∩DE=D，∴BC⊥平面PBD，∴BC⊥BD．
∵AB=AD=1，AB∥CD，
∴∠CDB=∠DBA=45°，∴BC=BD=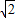
，
∵BC⊥BD，∴CD=2；
（2）解：∵PD⊥底面ABCD，∴CD⊥PD
∵CD⊥AD，AD∩PD=D，∴CD⊥平面PAD
延长DA，CB交于G，连接PG，则PG是所求二面角的棱．
作DH⊥PG于H，连接CH，根据三垂线定理，CH⊥PG，
∴∠CHD是侧面PAD与侧面PBC所成二面角的平面角，
∵PD=1，GD=2，∴DH=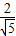
，
∵CD=2，∴tan∠CHD=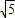
，
∴侧面PAD与侧面PBC所成锐二面角的大小为arctan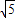
．
点评：本题考查线面垂直，考查面面角，考查学生的计算能力，正确作出面面角是关键．
（2）延长DA，CB交于G，连接PG，作DH⊥PG于H，连接CH，则可得∠CHD是侧面PAD与侧面PBC所成二面角的平面角，由此能求出侧面PAD与侧面PBC所成锐二面角的大小．
解答：
（1）证明：作DE⊥PB于E，∵平面PBC⊥平面PBD，∴DE⊥平面PBC，∴DE⊥BC．
∵PD⊥BC，PD∩DE=D，∴BC⊥平面PBD，∴BC⊥BD．
∵AB=AD=1，AB∥CD，
∴∠CDB=∠DBA=45°，∴BC=BD=
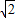，∵BC⊥BD，∴CD=2；
（2）解：∵PD⊥底面ABCD，∴CD⊥PD
∵CD⊥AD，AD∩PD=D，∴CD⊥平面PAD
延长DA，CB交于G，连接PG，则PG是所求二面角的棱．
作DH⊥PG于H，连接CH，根据三垂线定理，CH⊥PG，
∴∠CHD是侧面PAD与侧面PBC所成二面角的平面角，
∵PD=1，GD=2，∴DH=
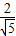，∵CD=2，∴tan∠CHD=
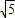，∴侧面PAD与侧面PBC所成锐二面角的大小为arctan
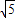．点评：本题考查线面垂直，考查面面角，考查学生的计算能力，正确作出面面角是关键．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．